這篇文章將要介紹梅森素數的定義以及在Python中實現的方法。
梅森數(Mn)指的是形如2n - 1的正整數,其中指數 n 是素數。
如果一個梅森數是素數,則稱其為梅森素數。例如22-1=3、23-1=7都是梅森素數。
當n=2,3,5,7時,Mn都是素數,但n = 11時,Mn = M11 = 211 - 1 = 2047 = 23 × 89,顯然 M11 不是梅森素數。
目前僅發現 51 個梅森素數,最大的是 M82589933 (即2的82589933次方減1),有24862048位。
梅森素數歷來都是數論研究中的一項重要內容,也是當今科學探索中的熱點和難點問題。
(以上來自 @潘石屹 微博話題 #潘石屹用Python解決100個問題#)
以下是實現求指數 n < 20 以內的所有梅森素數的源代碼。
import math
# 定義判斷一個數是否為素數的函數
def isprime(num):
tmp = int(math.sqrt(num))
for i in range(2, tmp + 1):
if num % i == 0:
return False
return True
N = 20 # 定義指數n的最大值
for n in range(2, N + 1):
if isprime(n): # 指數n是否為素數
mn = pow(2, n) - 1 # 求出梅森數
if isprime(mn): # 梅森數也是素數,則輸出
print(f"n={n}, M{n}={mn}")
以上程序執行的結果如下:
n=2, M2=3從運行結果來看,指數為20以內的梅森素數共7個。你可以接著往下找,第8個是 M31 = 21 4748 3647,第9個是M61 = 230 5843 0092 1369 3951,再下一個,武林網VEVB沒找出來,指數是不是在100以內也不知道。
n=3, M3=7
n=5, M5=31
n=7, M7=127
n=13, M13=8191
n=17, M17=131071
n=19, M19=524287
因為梅森素數很稀有,尋找起來也很費時,上面查找指數在20以內的梅森素數在個人電腦上約在1秒左右就可以完成。第8個約需要0.35秒,第9個約需130秒,下一個運行了很長時間,改進了求素數的算法,仍然沒有找出來。下圖是在運行多次后截圖的情況:
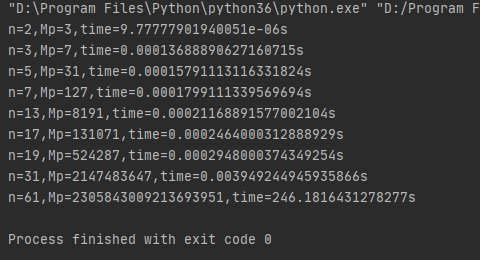
本文(完)
新聞熱點
疑難解答