集中趨勢(shì)是指一組數(shù)據(jù)向某一中心值靠攏或集中的程度。主要包括平均值、眾數(shù)、中位數(shù)和分位數(shù)。

先普及一下幾個(gè)概念：

（1）總體

在數(shù)理統(tǒng)計(jì)中，我們把研究對(duì)象的全體元素構(gòu)成的集合稱為總體（或母體），而把組成總體的每個(gè)元素稱為個(gè)體。如果總體包含有限個(gè)個(gè)體，則稱為有限總體（或具體總體）。如果總體包含無限個(gè)個(gè)體，則稱為無限總體（或抽象總體）。

（2）樣本

把從總體X中隨機(jī)抽檢（或觀察）n個(gè)個(gè)體的試驗(yàn)，稱為隨機(jī)抽樣，簡(jiǎn)稱抽樣，n稱為容量。

（3）樣本均值

設(shè)X₁, X₂, ..., X_n是總體X中的一個(gè)樣本，則統(tǒng)計(jì)量

（4）一組數(shù)據(jù)中出現(xiàn)次數(shù)最多的觀測(cè)值叫做眾數(shù)，用M₀表示。眾數(shù)測(cè)度數(shù)據(jù)的集中性趨勢(shì)，一般在數(shù)據(jù)量較大的情況下，眾數(shù)比較有意義。

（5）中位數(shù)

中位數(shù)簡(jiǎn)單講就是數(shù)據(jù)排序位于中間位置的值，記為M_e，即統(tǒng)計(jì)量

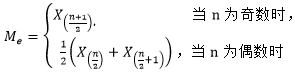
 中位數(shù)描述數(shù)據(jù)中心位置，對(duì)于對(duì)稱分布的數(shù)據(jù)，均值接近中位數(shù)；偏態(tài)分布式指頻數(shù)分布不對(duì)稱，集中位置偏向一側(cè)，數(shù)據(jù)的均值則與中位數(shù)不同。它的顯著特點(diǎn)在于不受異常值的影響，具有穩(wěn)健性。

（6）分位數(shù)

統(tǒng)計(jì)量

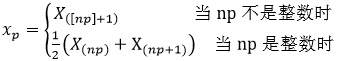
稱為樣本的p分位數(shù)。常用的有五分位數(shù)，由次序樣本的前0%,25%, 75%, 100%位置的5個(gè)數(shù)構(gòu)成。

下面探討在R語言中，如何實(shí)現(xiàn)。

（1）樣本均值

在R中，mean()函數(shù)用于計(jì)算樣本的均值，其使用格式為：

mean(x, trim=0, na.rm = FALSE, ...)

其中，參數(shù)x為計(jì)算對(duì)象，可以是向量、矩陣、數(shù)組或數(shù)據(jù)框；trim用于設(shè)置計(jì)算均值前去掉兩端數(shù)據(jù)的百分比，即計(jì)算結(jié)尾均值，取值在0~0.5之間；na.rm為邏輯值，指示是否允許有缺失值(NA)的情況，默認(rèn)為FALSE（不允許）;...為附加參數(shù)，

樣本均值舉例如下：

某班級(jí)20名學(xué)生的英語成績(jī)?yōu)?8,78,67,69,62,100,73,45,70,60,93,97,84,82,81,73,68,76,77,92。計(jì)算其均值

x<-c(88,78,67,69,62,100,73,45,70,60,93,97,84,82,81,73,68,76,77,92)
mean(x)

結(jié)果是76.75

如計(jì)算結(jié)尾，則：

mean(x,trim=0.05)

則結(jié)果是:77.22

（2）計(jì)算眾數(shù)

在R中，沒有給出直接計(jì)算眾數(shù)的函數(shù)，自己可以編寫函數(shù)，或使用下面的語句獲取眾數(shù)。

tmp<-table(x)  #計(jì)算出x中每個(gè)值出現(xiàn)的次數(shù)
index<-which.max(tmp)  #找出最多次數(shù)的索引
tmp[index]  #輸出對(duì)應(yīng)的數(shù)據(jù)及次數(shù)

本例的結(jié)果形式如下：

73
  2

但此方法只能適用于求一個(gè)眾數(shù)的情況。如果想找出具有多個(gè)眾數(shù)（即有多個(gè)數(shù)據(jù)的頻率相同且為最大者）的情況，可以使用下面的語句：

tmp<-table(x)
tmp.max<-max(tmp)
which(tmp==tmp.max)

若果令向量x的值為：12, 14, 16, 12, 15, 12, 15, 15；則會(huì)輸出如下結(jié)果：

12    15
  1      3

（3）計(jì)算中位數(shù)

在R中，使用median()函數(shù)計(jì)算一組數(shù)據(jù)的中位數(shù)。其形式如下：

median(x, na.rm = FALSE, ...)

各參數(shù)的含義與求均值函數(shù)mean()相同。

接均值的例子：

median(x)

結(jié)果為：76.5

由均值(76.75)和中位數(shù)(76.5)可知，均值稍大于中位數(shù)，可以初步判斷，所給樣本數(shù)據(jù)呈右偏分布。

（4）計(jì)算分位數(shù)

R中使用quantile()計(jì)算分位數(shù)，其形式如下：

quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE, names = TRUE, type = 7, ...)

其中，參數(shù)x為數(shù)據(jù)對(duì)象；probs給出相應(yīng)的百分位數(shù)；na.rm表示是否允許包含缺失值；names為邏輯值，指示是否為結(jié)果給出命名屬性；type為分為數(shù)的算法，取值1~9，默認(rèn)為7。

接均值的例子計(jì)算

quantile(x)
quantile(x,names=FALSE) #去掉各值的名字
fivenum(x)  #使用次函數(shù)可以直接計(jì)算出五個(gè)數(shù)
summary(x) #使用該函數(shù)可以計(jì)算出五數(shù)及均值

結(jié)果形式如下：

從結(jié)果中可以看出：quantile()函數(shù)默認(rèn)可以直接計(jì)算出五個(gè)數(shù)：最小值、25%的四分位數(shù)、中位數(shù)、75%的四分位數(shù)和最大值。