描述樣本值的離散程度,最常用的指標是方差和標準差,它們與前面所說的全距(極差)只使用了兩個極值情況不同,它們利用了樣本的全部信息去描述數據取值的分散性。
方差是各樣本相對均值的偏差平方和的平均。使用s2來表示,其公式如下:
![]()
當數據分布比較分散(即數據在平均數附近波動較大)時,各個數據與平均數的差的平方和較大,方差就較大;當數據分布比較集中時,各個數據與平均數的差的平方和較小。因此方差越大,數據的波動越大;方差越小,數據的波動就越小。
樣本方差的開方稱為樣本標準差,記為s,其計算公式如下:
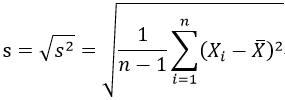
標準差越大,數據的離散程度越大,反之越小。但標準差與方差不同的地方是,標準差是有量綱的,它與變量值的計量單位相同,因此具有較強的實際意義,在實際應用較廣泛。

在R中使用var函數和sd函數分別計算方差和標準差。
var函數的語法形式如下:
var(x, y = NULL, na.rm = FALSE, use)
參數x是一個數值型向量,矩陣或數據框;
參數y是與x維度相容的一個向量、矩陣或數據框,默認為NULL值;
na.rm為邏輯值,指示是否移除缺失值,默認為FALSE;
use是一個可選參數,是一個字符型字符串。用于指明在有缺失值時計算協方差的方法。只能是 "everything", "all.obs", "complete.obs", "na.or.complete", or "pairwise.complete.obs"中值之一。
sd函數的語法形式如下:
sd(x, na.rm = FALSE)
各參數的含義與var函數對應的參數相同,但是x是一個數值型向量。
下面使用一個例子來說明具體使用方法。
設從某班某門課程中隨機抽取了20個學生的成績,具體如下:
51,99,65,100,68,84,72,85,78,64,69,95,90,75,66,50,63,55,64,70.
計算其方差和標準差。
編寫R程序如下:
grade <- c(51,99,65,100,68,84,72,85,78,64,69,95,90,75,66,50,63,55,64,70)
ss <- var(grade)
s <- sd(grade)
print(ss)
print(s)
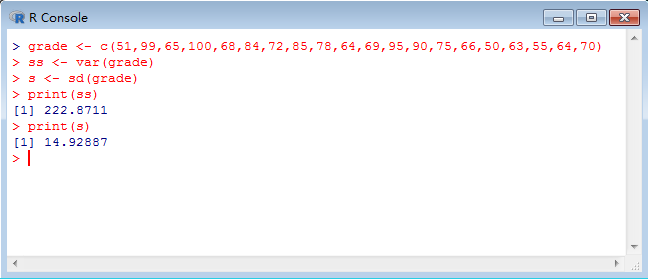
計算結果如下圖所示:
即方差為:222.87,標準差為:14.93
新聞熱點
疑難解答