錄一段音頻,把它的音高改變50次并把每一個(gè)新的音頻匹配到鍵盤(pán)的一個(gè)鍵位,你就能把電腦變成一架鋼琴!
一段音頻可以被編碼為一組數(shù)值的數(shù)組(或者列表),像這樣:

我們可以在數(shù)組中每隔一秒拿掉一秒的值來(lái)將這段音頻的速度變成兩倍。
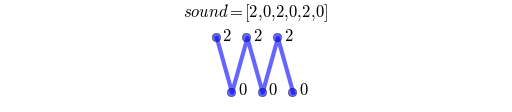
如此我們不僅將音頻的長(zhǎng)度減半了,而且我們還將它的頻率翻倍了,這樣使得它擁有比原來(lái)更高的音高(pitch)。
相反地,假如我們將數(shù)組中每個(gè)值重復(fù)一次,我們將得到一段更慢,周期更長(zhǎng),即音高更低的音頻:

這里提供一個(gè)可以按任意系數(shù)改變音頻速度的任意簡(jiǎn)單的Python函數(shù):
import numpy as np def speedx(sound_array, factor): """ 將音頻速度乘以任意系數(shù)`factor` """ indices = np.round( np.arange(0, len(snd_array), factor) ) indices = indices[indices < len(snd_array)].astype(int) return sound_array[ indices.astype(int) ]
這個(gè)問(wèn)題更困難的地方在于改變音頻長(zhǎng)度的同時(shí)保持它的音高(變速,音頻拉伸(sound stretching)),或者在改變音頻的音高的同時(shí)保持它的長(zhǎng)度(變調(diào)(pitch shifting))。
變速
變速可以通過(guò)傳統(tǒng)的相位聲碼器(phase vocoder,感興趣的朋友可以讀一下維基百科的頁(yè)面)來(lái)實(shí)現(xiàn)。首先將音頻分解成重疊的比特,然后將這些比特重新排列使得他們重疊得更多(將縮短聲音的長(zhǎng)度)或者更少(將拉伸音頻的長(zhǎng)度),如下圖所示:
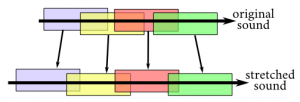
困難之處在于重新排列的比特可能很?chē)?yán)重的互相影響,那么這里就需要用到相位變換來(lái)確保它們之間沒(méi)有影響。這里有一段Python代碼,取自這個(gè)網(wǎng)頁(yè)(打不開(kāi)的話,您懂的。――譯者注):
def stretch(sound_array, f, window_size, h): """ 將音頻按系數(shù)`f`拉伸 """ phase = np.zeros(window_size) hanning_window = np.hanning(window_size) result = np.zeros( len(sound_array) /f + window_size) for i in np.arange(0, len(sound_array)-(window_size+h), h*f): # 兩個(gè)可能互相重疊的子數(shù)列 a1 = sound_array[i: i + window_size] a2 = sound_array[i + h: i + window_size + h] # 按第一個(gè)數(shù)列重新同步第二個(gè)數(shù)列 s1 = np.fft.fft(hanning_window * a1) s2 = np.fft.fft(hanning_window * a2) phase = (phase + np.angle(s2/s1)) % 2*np.pi a2_rephased = np.fft.ifft(np.abs(s2)*np.exp(1j*phase)) # 加入到結(jié)果中 i2 = int(i/f) result[i2 : i2 + window_size] += hanning_window*a2_rephased result = ((2**(16-4)) * result/result.max()) # 歸一化 (16bit) return result.astype('int16')
變調(diào)
一旦你實(shí)現(xiàn)了變速以后,變調(diào)就不難了。如果需要一個(gè)更高的音高,可以先將這段音頻拉伸并保持音高不變,然后再加快它的速度,如此最后得到的音頻將具有原始音頻同樣的長(zhǎng)度,更高的頻率,即更高的音高。
把一段音頻的頻率翻倍將把音高提高一個(gè)八度,也就是12個(gè)半音。因此,要將音高提高n個(gè)半音的話,我們需要將頻率乘上系數(shù)2^(n/12):
新聞熱點(diǎn)
疑難解答
圖片精選