線性判別分析（linear discriminant analysis），LDA。也稱為Fisher線性判別（FLD）是模式識別的經典算法。

（1）中心思想：將高維的樣本投影到最佳鑒別矢量空間，來達到抽取分類信息和壓縮特種空間維數的效果，投影后保證樣本在新的子空間有最大的類間距離和最小的類內距離。也就是說在該空間中有最佳的可分離性。

（2）與PCA的不同點：PCA主要是從特征的協方差出發，來找到比較好的投影方式，最后需要保留的特征維數可以自己選擇。但是LDA更多的是考慮了類別信息，即希望投影后不同類別之間數據點的距離更大，同一類別的數據點更緊湊。

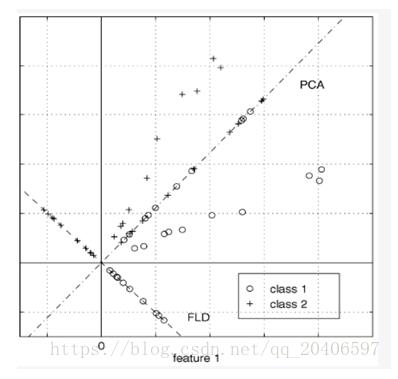
從圖中也可以看出，LDA的投影后就已經將不同的類別分開了。

所以說，LDA是以分類為基準的，考慮的是如何選擇投影方向使得分類更好，是有監督的。但是PCA是一種無監督的降維方式，它只是單純的降維，只考慮如何選擇投影面才能使得降維以后的樣本信息保留的最大。

（3）LDA的維度：LDA降維后是與類別個數直接相關的，而與數據本身的維度沒有關系。如果有C個類別，LDA降維后一般會選擇1-C-1維。對于很多二分類問題，LDA之后就剩下一維，然后再找到一個分類效果最好的閾值就可以進行分類了。

（4）投影的坐標系是否正交：

PCA的投影坐標系都是正交的，而LDA是根據類別的標注，主要關注的是分類能力，因此可以不去關注石否正交，而且一般都不正交。

（5）LDA步驟：

（a）計算各個類的樣本均值：

這個地方需要注意的是，分別求出每個類別樣本的Sbi或者Swi后，在計算總體的Sb和Sw時需要做加權平均，因為每個類別中的樣本數目可能是不一樣的。

（d）LDA作為一個分類的算法，我們希望類內的聚合度高，即類內散度矩陣小，而類間散度矩陣大。這樣的分類效果才好。因此引入Fisher鑒別準則表達式：

（inv(Sw)Sb）的特征向量。且最優投影軸的個數d<=C-1;

（e）所以，只要計算出矩陣inv(Sw)Sb的最大特征值對應的特征向量，該特征向量就是投影方向W。

（6）計算各點在投影后的方向上的投影點：

MATLAB實現代碼：

%這是訓練數據集%2.9500 6.6300 0%2.5300 7.7900 0%3.5700 5.6500 0%3.1600 5.4700 0%2.5800 4.4600 1%2.1600 6.2200 1%3.2700 3.5200 1X=load('22.txt');pos0=find(X(:,3)==0);pos1=find(X(:,3)==1);X1=X(pos0,1:2);X2=X(pos1,1:2);hold onplot(X1(:,1),X1(:,2),'r+','markerfacecolor', [ 1, 0, 0 ]);plot(X2(:,1),X2(:,2),'b*','markerfacecolor', [ 0, 0, 1 ]);grid on%輸出樣本的二維分布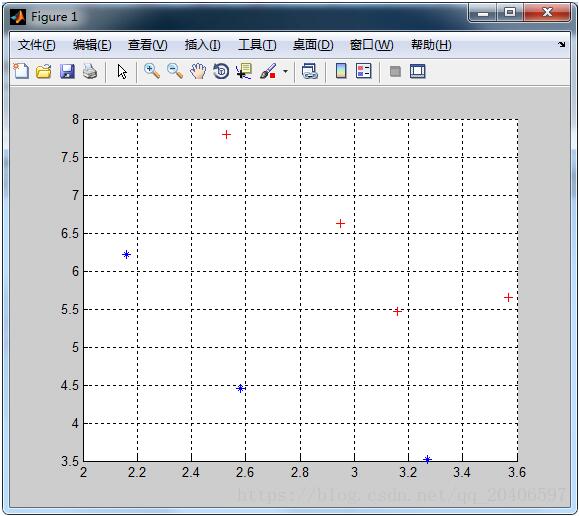

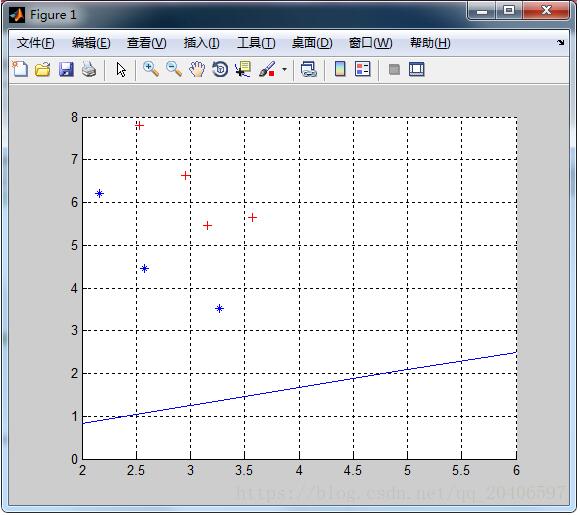
M1 = mean(X1);M2 = mean(X2);M = mean([X1;X2]);%第二步：求類內散度矩陣p = size(X1,1);q = size(X2,1);a=repmat(M1,4,1);S1=(X1-a)'*(X1-a);b=repmat(M2,3,1);S2=(X2-b)'*(X2-b);Sw=(p*S1+q*S2)/(p+q);%第三步：求類間散度矩陣sb1=(M1-M)'*(M1-M);sb2=(M2-M)'*(M2-M);Sb=(p*sb1+q*sb2)/(p+q);bb=det(Sw);%第四步：求最大特征值和特征向量[V,L]=eig(inv(Sw)*Sb);[a,b]=max(max(L));W = V(:,b);%最大特征值所對應的特征向量%第五步：畫出投影線k=W(2)/W(1);b=0;x=2:6;yy=k*x+b;plot(x,yy);%畫出投影線