總體思路與一元線性回歸思想一樣,現在將數據以矩陣形式進行運算,更加方便。
一元線性回歸實現代碼
下面是多元線性回歸用Python實現的代碼:
import numpy as npdef linearRegression(data_X,data_Y,learningRate,loopNum): W = np.zeros(shape=[1, data_X.shape[1]]) # W的shape取決于特征個數,而x的行是樣本個數,x的列是特征值個數 # 所需要的W的形式為 行=特征個數,列=1 這樣的矩陣。但也可以用1行,再進行轉置:W.T # X.shape[0]取X的行數,X.shape[1]取X的列數 b = 0 #梯度下降 for i in range(loopNum): W_derivative = np.zeros(shape=[1, data_X.shape[1]]) b_derivative, cost = 0, 0 WXPlusb = np.dot(data_X, W.T) + b # W.T:W的轉置 W_derivative += np.dot((WXPlusb - data_Y).T, data_X) # np.dot:矩陣乘法 b_derivative += np.dot(np.ones(shape=[1, data_X.shape[0]]), WXPlusb - data_Y) cost += (WXPlusb - data_Y)*(WXPlusb - data_Y) W_derivative = W_derivative / data_X.shape[0] # data_X.shape[0]:data_X矩陣的行數,即樣本個數 b_derivative = b_derivative / data_X.shape[0] W = W - learningRate*W_derivative b = b - learningRate*b_derivative cost = cost/(2*data_X.shape[0]) if i % 100 == 0: print(cost) print(W) print(b)if __name__== "__main__": X = np.random.normal(0, 10, 100) noise = np.random.normal(0, 0.05, 20) W = np.array([[3, 5, 8, 2, 1]]) #設5個特征值 X = X.reshape(20, 5) #reshape成20行5列 noise = noise.reshape(20, 1) Y = np.dot(X, W.T)+6 + noise linearRegression(X, Y, 0.003, 5000)
特別需要注意的是要弄清:矩陣的形狀
在梯度下降的時候,計算兩個偏導值,這里面的矩陣形狀變化需要注意。
梯度下降數學式子:
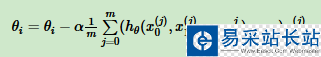
以代碼中為例,來分析一下梯度下降中的矩陣形狀。
代碼中設了5個特征。

WXPlusb = np.dot(data_X, W.T) + b
W是一個1*5矩陣,data_X是一個20*5矩陣
WXPlusb矩陣形狀=20*5矩陣乘上5*1(W的轉置)的矩陣=20*1矩陣
W_derivative += np.dot((WXPlusb - data_Y).T, data_X)
W偏導矩陣形狀=1*20矩陣乘上 20*5矩陣=1*5矩陣
b_derivative += np.dot(np.ones(shape=[1, data_X.shape[0]]), WXPlusb - data_Y)
b是一個數,用1*20的全1矩陣乘上20*1矩陣=一個數
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持武林站長站。
新聞熱點
疑難解答