本文實例為大家分享了tensorflow實現(xiàn)線性回歸的具體代碼，供大家參考，具體內(nèi)容如下

一、隨機生成1000個點，分布在y=0.1x+0.3直線周圍，并畫出來

import tensorflow as tfimport numpy as npimport matplotlib.pyplot as pltnum_points = 1000vectors_set = []for i in range(num_points):  x1 = np.random.normal(0.0,0.55)  //設(shè)置一定范圍的浮動  y1 = x1*0.1+0.3+np.random.normal(0.0,0.03)  vectors_set.append([x1,y1])x_data = [v[0] for v in vectors_set]y_data = [v[1] for v in vectors_set]plt.scatter(x_data,y_data,c='r')plt.show()

二、構(gòu)造線性回歸函數(shù)

#生成一維的w矩陣，取值為[-1，1]之間的隨機數(shù)w = tf.Variable(tf.random_uniform([1],-1.0,1.0),name='W')#生成一維的b矩陣，初始值為0b = tf.Variable(tf.zeros([1]),name='b')y = w*x_data+b#均方誤差loss = tf.reduce_mean(tf.square(y-y_data),name='loss')#梯度下降optimizer = tf.train.GradientDescentOptimizer(0.5)#最小化losstrain = optimizer.minimize(loss,name='train')sess=tf.Session()init = tf.global_variables_initializer()sess.run(init)#print("W",sess.run(w),"b=",sess.run(b),"loss=",sess.run(loss))for step in range(20):  sess.run(train)  print("W=",sess.run(w),"b=",sess.run(b),"loss=",sess.run(loss))//顯示擬合后的直線plt.scatter(x_data,y_data,c='r')plt.plot(x_data,sess.run(w)*x_data+sess.run(b))plt.show()

三、部分訓(xùn)練結(jié)果如下：

W= [ 0.10559751] b= [ 0.29925063] loss= 0.000887708W= [ 0.10417549] b= [ 0.29926425] loss= 0.000884275W= [ 0.10318361] b= [ 0.29927373] loss= 0.000882605W= [ 0.10249177] b= [ 0.29928035] loss= 0.000881792W= [ 0.10200921] b= [ 0.29928496] loss= 0.000881397W= [ 0.10167261] b= [ 0.29928818] loss= 0.000881205W= [ 0.10143784] b= [ 0.29929042] loss= 0.000881111W= [ 0.10127408] b= [ 0.29929197] loss= 0.000881066

擬合后的直線如圖所示：

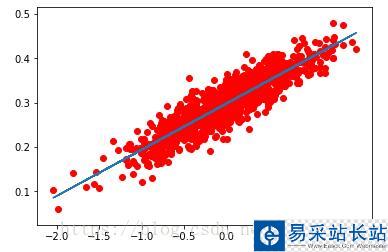
結(jié)論：最終w趨近于0.1，b趨近于0.3，滿足提前設(shè)定的數(shù)據(jù)分布

以上就是本文的全部內(nèi)容，希望對大家的學(xué)習(xí)有所幫助，也希望大家多多支持武林站長站。