神經(jīng)網(wǎng)絡(luò)在機(jī)器學(xué)習(xí)中有很大的應(yīng)用，甚至涉及到方方面面。本文主要是簡單介紹一下神經(jīng)網(wǎng)絡(luò)的基本理論概念和推算。同時(shí)也會介紹一下神經(jīng)網(wǎng)絡(luò)在數(shù)據(jù)分類方面的應(yīng)用。

首先，當(dāng)我們建立一個(gè)回歸和分類模型的時(shí)候，無論是用最小二乘法（OLS）還是最大似然值（MLE）都用來使得殘差達(dá)到最小。因此我們在建立模型的時(shí)候，都會有一個(gè)loss function。

而在神經(jīng)網(wǎng)絡(luò)里也不例外，也有個(gè)類似的loss function。

對回歸而言：

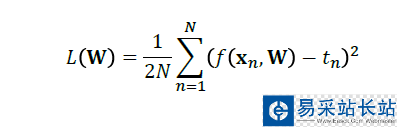
對分類而言：

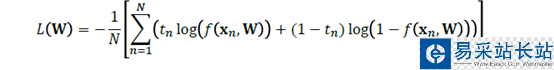
然后同樣方法，對于W開始求導(dǎo)，求導(dǎo)為零就可以求出極值來。

關(guān)于式子中的W。我們在這里以三層的神經(jīng)網(wǎng)絡(luò)為例。先介紹一下神經(jīng)網(wǎng)絡(luò)的相關(guān)參數(shù)。

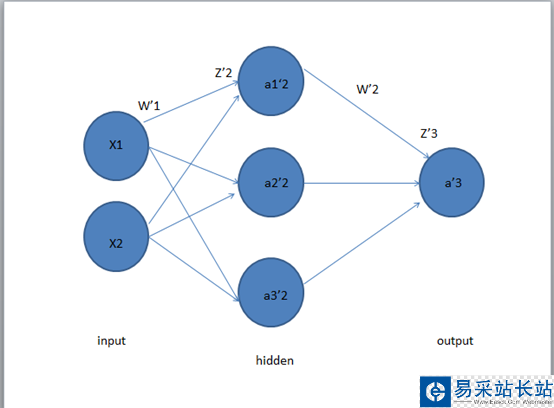
第一層是輸入層，第二層是隱藏層，第三層是輸出層。

在X1，X2經(jīng)過W1的加權(quán)后，達(dá)到隱藏層，然后經(jīng)過W2的加權(quán)，到達(dá)輸出層

其中，

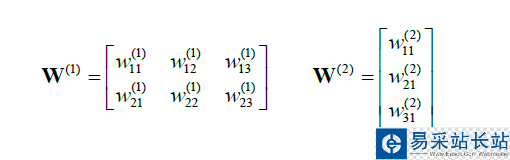
我們有：

至此，我們建立了一個(gè)初級的三層神經(jīng)網(wǎng)絡(luò)。

當(dāng)我們要求其的loss function最小時(shí)，我們需要逆向來求，也就是所謂的backpropagation。

我們要分別對W1和W2進(jìn)行求導(dǎo)，然后求出其極值。

從右手邊開始逆推，首先對W2進(jìn)行求導(dǎo)。

代入損失函數(shù)公式：

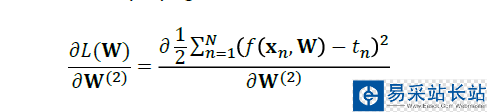
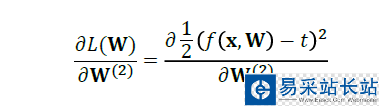
然后，我們進(jìn)行化簡：

化簡到這里，我們同理再對W1進(jìn)行求導(dǎo)。

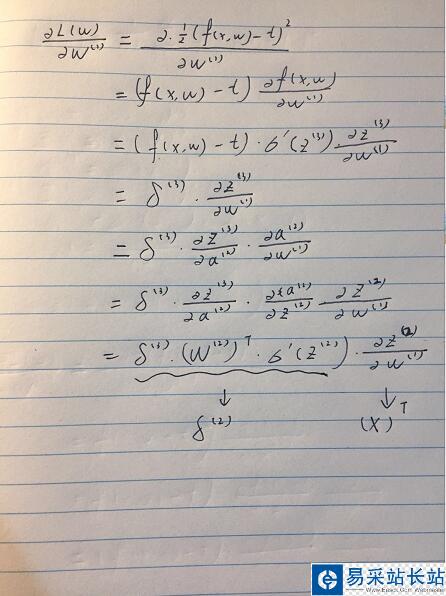
我們可以發(fā)現(xiàn)當(dāng)我們在做bp網(wǎng)絡(luò)時(shí)候，有一個(gè)逆推回去的誤差項(xiàng)，其決定了loss function 的最終大小。

在實(shí)際的運(yùn)算當(dāng)中，我們會用到梯度求解，來求出極值點(diǎn)。

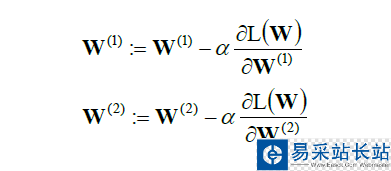
總結(jié)一下來說，我們使用向前推進(jìn)來理順神經(jīng)網(wǎng)絡(luò)做到回歸分類等模型。而向后推進(jìn)來計(jì)算他的損失函數(shù)，使得參數(shù)W有一個(gè)最優(yōu)解。

當(dāng)然，和線性回歸等模型相類似的是，我們也可以加上正則化的項(xiàng)來對W參數(shù)進(jìn)行約束，以免使得模型的偏差太小，而導(dǎo)致在測試集的表現(xiàn)不佳。