泊松分布(Poisson Distribution)是一種離散型概率分布。泊松分布是描述某一特定時間或空間段內,某一事件發生的次數的分布。如機器每周發生故障的次數,某醫院婦產科2小時內出生的嬰兒個數,某服務臺在某時間段內到達的顧客次數等。
泊松(Poisson)分布的分布律為:
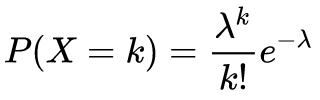
其中 ,則稱X服從參數為
,則稱X服從參數為 的泊松分布,記為
的泊松分布,記為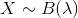 或
或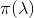 。
。
這里的P即為等同區間內事件發生k次的概率;
X:事件次數的變量;
k:事件發生的次數,取值為0,1,2,3...
λ:區間內事件發生的平均次數(數學期望)
同時,顯然有:

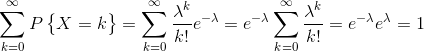
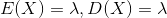
(1)事件發生是小概率事件;
(2)事件的發生是相互獨立的;
(3)事件在任意兩個等同的區間內發生的概率是穩定的。
(1)泊松分布是一種描述和分析稀有事件的概率分布。要觀察到這類事件,樣本含量n必須很大。
(2)λ是泊松分布所依賴的唯一參數。λ值愈小,分布愈偏倚,隨著λ的增大,分布趨于對稱。
(3)當λ = 20時,泊松分布接近于正態分布;當λ = 50時,可以認為泊松分布呈正態分布。在實際工作中,當λ≥20時就可以用正態分布來近似地處理泊松分布的問題。
1、相關函數
在R中,pois表示泊松分布,加上不同的前綴表示不同的函數,加上前綴d表示概率密度函數,加上前綴p表示分布函數,加前綴q表示分位函數,加前綴r表示隨機生成數,各函數的語法格式如下:
dpois( x, lambda, log = FALSE ) #發生x次隨機事件的概率
ppois( q, lambda, lower.tail = TRUE, log.p = FALSE ) # 至多發生q次事件的累計概率
qpois( p, lambda, lower.tail = TRUE, log.p = FALSE ) #在p概率下事件發生的次數
rpois( n, lambda ) #重復n組試驗,每組發生隨機事件的次數
函數中各參數的含義:
幾點說明:
(1)若x為非整數,dpois 的結果將會使0,并給出一個警告錯誤;
(2)分位數是右連續的,qpois(p, lambda) 表示x是最小整數的情況:P(X ≤ x) ≥ p;
(3)設置lower.tail = FALSE,可以得到更加精確的結果,而lower.tail = TRUE將返回1;
(4)無效的lambda值,將會返回NaN,并給出警告錯誤。
2、使用示例
(1)某銀行,顧客到達柜臺的平均值是5分鐘3.2名,計算:①接下來5分鐘內,有0名顧客、1名顧客和2名顧客到達的概率分別是多少?②在5分鐘內至多有7名顧客到達的概率是多少?③在5分鐘內有7名以上顧客到達的概率是多少?④在90%的概率下,5分鐘內至多有幾名顧客到達?
編寫R程序如下:
lmbda <- 3.2
# 5分鐘內0名、1名、2名顧客的概率
dpois(0:2, lmbda)
# 5分鐘至多7名顧客的概率
ppois(7, lmbda)
# 5分鐘有7名以上顧客到達的概率
1 - ppois(7, lmbda)
# 90%概率下,5分鐘內至多有幾名顧客到達
qpois(0.9, lmbda)
運行結果如下圖所示:

(2)某工廠某種設備每周的平均故障臺數為2.3臺,求下周該設備沒有發生故障的概率,下周至多有3臺發生故障的概率;重復模擬10組試驗,每組發生故障的臺數是多少
編寫R程序如下:
lambda <- 2.3
# 下周沒有設備發生故障的概率
dpois(0, lambda)
#下周至多有3臺設備發生故障的概率
ppois(3, lambda)
#重復1000組試驗,每組發生故障的臺數
rpois(10, lambda)
在R中運行的結果如下圖所示:

我們也可以使用R繪制出泊松分布的概率密度圖,下例演示了均值為2,重復1000次情況下的直方圖。
x <- rpois(1000, 2)
hist(x)
繪圖結果之一如下(因為隨機生成,每次的結果并不一定相同):

本文(完)
新聞熱點
疑難解答