均勻分布也稱矩形分布,是最簡單的一種連續型分布。
若隨機變量X的概率密度函數為:
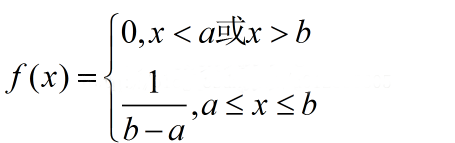
則稱X服從區間[a, b]上的均勻分布,記為X~U[a, b]。
概率密度圖像如下圖所示:
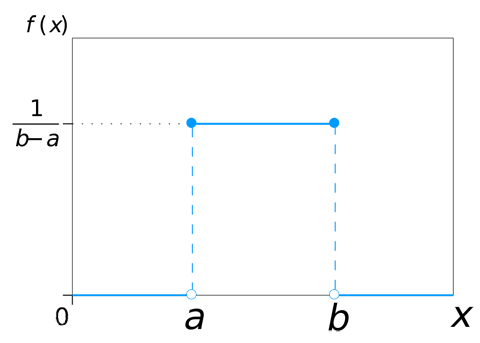
其分布函數為:
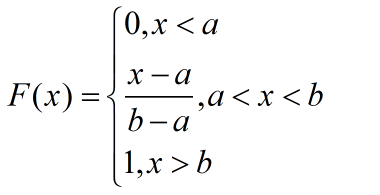
分布函數是概率密度函數從負無窮到正無窮上的積分;在坐標軸上,概率密度函數的函數值y表示落在x點上的概率為y;分布函數的函數值y則表示x落在區間(-∞,+∞)上的概率。
分布函數圖像如下圖所示:
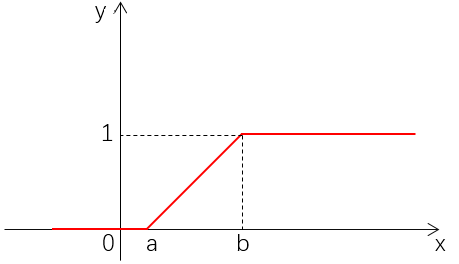
均勻分布的數學期望與方差分別為:
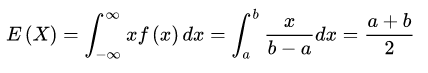
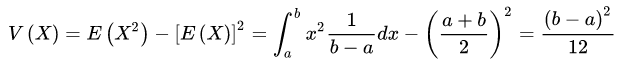
在R中,unif是用來進行均勻分布分析的,在其前面加上不同的前綴表示不同的函數,各函數的使用格式如下所示:
dunif(x, min = 0, max = 1, log = FALSE) # 分布密度
punif(q, min = 0, max = 1, lower.tail = TRUE, log.p = FALSE) # 分布函數
qunif(p, min = 0, max = 1, lower.tail = TRUE, log.p = FALSE) # 分位數函數
runif(n, min = 0, max = 1) # 隨機數產生函數
各參數的主要含義如下:
x, q : 數值向量
p : 概率向量
n : 觀測次數值
min, max : 均勻分布的下限和上限,必須是有限的值,min相當于密度函數或分布函數中的a,默認值為0,max相當于b,默認值為1;
log, log.p: 邏輯值,默認為FALSE.指定為TRUE時,概率值p是以log(p)給出的;
lower.tail : 邏輯值,默認為TRUE. 指定為TRUE時,概率是P [ X ≤ x ],否則是 P [ X > x ].
設電阻R是隨機變量,其值均勻分布在900Ω~1100Ω。
(1)求該區間內的分布密度;
(2)求電阻不超過950Ω的概率;
(3)求電阻超過950Ω的概率;
(4)在90%概率下,電阻值最大為多少;
(5)隨機生成5個符合該均勻分布的電阻值。
由題意可知:其分布函數 f(r) = 1/(1100-900) = 1/200 ( 900 ≤ r ≤ 1100)
(1)因為是均勻分布,使用R語言進行求值時,選取[900, 1100]中任何一個值,其概率密度值都是一樣的。
(2)即求 P(r ≤ 950)的概率,使用分布函數可以方便求出;
(3)即求p(r>950)的概率,可以使用 1 - p(r≤950) 計算得出。
(4)實際上相當于“電阻值不大于r的概率是90%,求x”,可以使用分位函數來求;
(5)使用runif()函數可以獲得這樣的隨機值。
編寫R程序如下:
a <- 900
b <- 1100
# 計算概率密度
f <- dunif(900, a, b)
cat("概率密度為:", f, "/n")
p <- punif(950, a, b)
cat("電阻不超過950歐姆的概率為:", p, "/n")
p <- 1 - punif(950, a, b)
cat("電阻超過950歐姆的概率為:", p, "/n")
R <- qunif(0.9, a, b)
cat("90%概率下,電阻值最大為:", R, "/n")
# 隨機生成5個符合該均勻分布的隨機電阻值
runif(5, a, b)
在R運行結果如下圖所示:

本文(完)
新聞熱點
疑難解答