數(shù)據(jù)庫的關(guān)系運(yùn)算中,專門的關(guān)系運(yùn)算包括選擇,投影,連接和除。本文講解一下除運(yùn)算的原理。
在講解除運(yùn)算之前,先介紹一下象集的概念。
關(guān)于像集的概念:
給定一個(gè)關(guān)系R(X,Z),X和Z為屬性組,當(dāng)t[X] = x時(shí),x在R中的像集(Images Set)為:
ZX={t[Z]|t∈R,t[X] = x}
它表示R中屬性組X上值為x的諸元組在Z上分量的集合。
關(guān)系除運(yùn)算的定義:
關(guān)系的除運(yùn)算是同時(shí)從關(guān)系的水平方向和垂直方向上進(jìn)行的運(yùn)算。假設(shè)關(guān)系R(X,Y)和S(Y,Z),X、Y、Z為屬性組。R÷S應(yīng)當(dāng)滿足元組在X上的分量值X的像集YX包含關(guān)系S在屬性組Y上投影的集合。其形式定義為:
R÷S = {tn[X]|tn∈R^πY(S)⊆YX}
R與S的除運(yùn)算得到一個(gè)新的關(guān)系P(X),P是R中滿足下列條件的元組在X屬性列上的投影:
關(guān)系R(X,Y)和S(Y,Z),其中X,Y,Z為屬性組(R中的Y與S中的Y可以有不同的屬性名,但必須出自相同的域集);
元組在X上的分量值X 的像集YX包含S在Y上的投影。
下面以一個(gè)例子來說明:
假設(shè)關(guān)系R和S如下:

計(jì)算R÷S的過程:
a1的象集為{(b1,c2),(b2,c3),(b2,c1)}
a2的象集為{(b3,c7),(b2,c3)}
a3的象集為{(b4,c6)}
a4的象集為{(b6,c6)}
S在(B,C)上的投影為:
{(b1,c2),(b2,c1),(b2,c3)}
因?yàn)橹挥衋1的象集包含了S在(B,C)屬性組上的投影,故R÷S={a1},即:
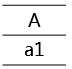
R÷S的結(jié)果為:
|
新聞熱點(diǎn)
疑難解答