先前說了樹的基本操作,我們采用的是二叉鏈表來保存樹形結構,當然二叉有二叉的困擾之處,比如我想找到當前結點的“前驅”和“后繼”,那么我們就必須要遍歷一下樹,然后才能定位到該“節點”的“前驅”和“后繼”,每次定位都是O(n),這不是我們想看到的,那么有什么辦法來解決呢?
(1) 在節點域中增加二個指針域,分別保存“前驅”和“后繼”,那么就是四叉鏈表了,哈哈,還是有點浪費空間啊。
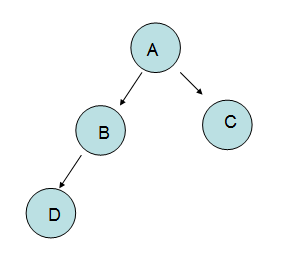
(2) 看下面的這個二叉樹,我們知道每個結點有2個指針域,4個節點就有8個指針域,其實真正保存節點的指針
僅有3個,還有5個是空閑的,那么為什么我們不用那些空閑的指針域呢,達到資源的合理充分的利用。
一: 線索二叉樹
1 概念
剛才所說的在空閑的指針域里面存放“前驅”和“后繼”就是所謂的線索。
<1> 左線索: 在空閑的左指針域中存放該“結點”的“前驅”被認為是左線索。
<2> 右線索: 在空閑的右指針域中存放該“結點“的”后繼“被認為是右線索。
當“二叉鏈表”被套上這種線索,就被認為是線索鏈表,當“二叉樹”被套上這種線索就被認為是線索二叉樹,當然線索根據
二叉樹的遍歷形式不同被分為“先序線索”,“中序線索”,“后序線索”。
2 結構圖
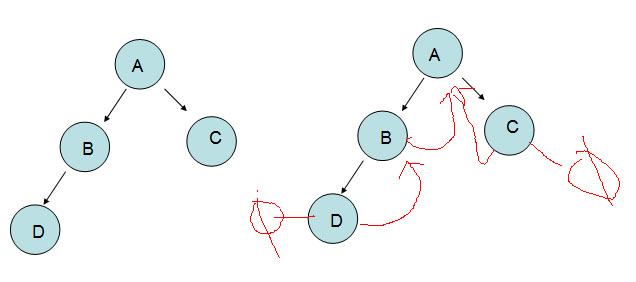
說了這么多,我們還是上圖說話,就拿下面的二叉樹,我們構建一個中序線索二叉樹,需要多動動腦子喲。
<1> 首先要找到“中序遍歷”中的首結點D,因為“D結點”是首節點,所以不存在“前驅”,左指針自然是空,
”D節點”的右指針存放的是“后繼”,那么根據“中序遍歷”的規則應該是B,所以D的右指針存放著B節點。
<2> 接著就是“B節點”,他的左指針不為空,所以就不管了,但是他的“右指針”空閑,根據規則“B結點“的右
指針存放的是"A結點“。
<3> 然后就是“A節點”,他已經被塞的滿滿的,所以就沒有“線索”可言了。
<4> 最后就是“C節點”,根據規則,他的“左指針”存放著就是“A節點“,”C節點“是最后一個節點,右指針自然就是空的,你懂的。
3 基本操作
常用的操作一般有“創建線索二叉樹”,”查找后繼節點“,”查找前驅節點“,”遍歷線索二叉樹“,下面的操作我們就以”中序遍歷“來創建中序線索二叉樹。
<1> 線索二叉樹結構
從“結構圖”中可以看到,現在結點的指針域中要么是”子節點(SubTree)“或者是”線索(Thread)“,此時就要設立標志位來表示指針域存放的是哪一種。
#region 線索二叉樹的結構
/// <summary>
/// 線索二叉樹的結構
/// </summary>
/// <typeparam name="T"></typeparam>
public class ThreadTree<T>
{
public T data;
public ThreadTree<T> left;
public ThreadTree<T> right;
public NodeFlag leftFlag;
public NodeFlag rightFlag;
}
#endregion
<2> 創建線索二叉樹
剛才也說了如何構建中序線索二叉樹,在代碼實現中,我們需要定義一個節點來保存當前節點的前驅,我練習的時候迫不得已,只能使用兩個
ref來實現地址操作,達到一個Tree能夠讓兩個變量來操作。
//先左子樹遍歷,尋找起始點
BinTreeThreadingCreate_LDR(ref tree.left, ref prevNode);
//如果left為空,則說明該節點可以放“線索”
tree.leftFlag = (tree.left == null) ? NodeFlag.Thread : NodeFlag.SubTree;
//如果right為空,則說明該節點可以放“線索”
tree.rightFlag = (tree.right == null) ? NodeFlag.Thread : NodeFlag.SubTree;
if (prevNode != null)
{
if (tree.leftFlag == NodeFlag.Thread)
tree.left = prevNode;
if (prevNode.rightFlag == NodeFlag.Thread)
prevNode.right = tree;
}
//保存前驅節點
prevNode = tree;
BinTreeThreadingCreate_LDR(ref tree.right, ref prevNode);
}
#endregion
<3> 查找后繼結點
現在大家都知道,后繼結點都是保存在“結點“的右指針域中,那么就存在”兩種情況“。
《1》 拿“B節點“來說,他沒有右孩子,則肯定存放著線索(Thread),所以我們直接O(1)的返回他的線索即可。
《2》 拿“A節點”來說,他有右孩子,即右指針域存放的是SubTree,悲哀啊,如何才能得到“A節點“的后繼呢?其實也很簡單,
根據”中序“的定義,”A節點“的后繼必定是”A節點“的右子樹往左鏈找的第一個沒有左孩子的節點(只可意會,不可言傳,嘻嘻)。
//如果查找節點的標志域中是Thread,則直接獲取
if (tree.rightFlag == NodeFlag.Thread)
return tree.right;
else
{
//根據中序遍歷的規則是尋找右子樹中中序遍歷的第一個節點
var rightNode = tree.right;
//如果該節點是subTree就需要循環遍歷
while (rightNode.leftFlag == NodeFlag.SubTree)
{
rightNode = rightNode.left;
}
return rightNode;
}
}
#endregion
<4> 查找前驅節點
這個跟(3)的操作很類似,同樣也具有兩個情況。
《1》 拿“C結點”來說,他沒有“左子樹”,則說明“C節點”的左指針為Thread,此時,我們只要返回左指針域即可得到前驅結點。
《2》 拿"A節點“來說,他有”左子樹“,則說明”A節點“的左指針為SubTree,那么怎么找的到”A節點“的前驅呢?同樣啊,根據
”中序遍歷“的性質,我們可以得知在”A節點“的左子樹中往”右鏈“中找到第一個沒有”右孩子“的節點。
//如果標志域中存放的是線索,那么可以直接找出來
if (tree.leftFlag == NodeFlag.Thread)
return tree.left;
else
{
//根據”中序“的規則可知,如果不為Thread,則要找出左子樹的最后節點
//也就是左子樹中最后輸出的元素
var leftNode = tree.left;
while (leftNode.rightFlag == NodeFlag.SubTree)
leftNode = leftNode.right;
return leftNode;
}
}
#endregion
<5> 遍歷線索二叉樹
因為我們構建線索的時候采用的是“中序”,那么我們遍歷同樣采用“中序”,大家是否看到了“線索”的好處,此時我們找某個節點的時間復雜度變為了
O(1) ~0(n)的時間段,比不是線索的時候查找“前驅"和“后繼”效率要高很多。
while (tree.leftFlag == NodeFlag.SubTree)
tree = tree.left;
do
{
Console.Write(tree.data + "/t");
tree = BinTreeThreadNext_LDR(tree);
} while (tree != null);
}
#endregion
最后上一下總的運行代碼
namespace ThreadChainTree
{
class Program
{
static void Main(string[] args)
{
ThreadTreeManager manager = new ThreadTreeManager();
//生成根節點
ThreadTree<string> tree = CreateRoot();
//生成節點
AddNode(tree);
ThreadTree<string> prevNode = null;
//構建線索二叉樹
manager.BinTreeThreadingCreate_LDR(ref tree, ref prevNode);
Console.WriteLine("/n線索二叉樹的遍歷結果為:/n");
//中序遍歷線索二叉樹
manager.BinTreeThread_LDR(tree);
}
#region 生成根節點
/// <summary>
/// 生成根節點
/// </summary>
/// <returns></returns>
static ThreadTree<string> CreateRoot()
{
ThreadTree<string> tree = new ThreadTree<string>();
Console.WriteLine("請輸入根節點,方便我們生成樹/n");
tree.data = Console.ReadLine();
Console.WriteLine("根節點生成已經生成/n");
return tree;
}
#endregion
#region 插入節點操作
/// <summary>
/// 插入節點操作
/// </summary>
/// <param name="tree"></param>
static ThreadTree<string> AddNode(ThreadTree<string> tree)
{
ThreadTreeManager mananger = new ThreadTreeManager();
while (true)
{
ThreadTree<string> node = new ThreadTree<string>();
Console.WriteLine("請輸入要插入節點的數據:/n");
node.data = Console.ReadLine();
Console.WriteLine("請輸入要查找的父節點數據:/n");
var parentData = Console.ReadLine();
if (tree == null)
{
Console.WriteLine("未找到您輸入的父節點,請重新輸入。");
continue;
}
Console.WriteLine("請確定要插入到父節點的:1 左側,2 右側");
Direction direction = (Direction)Enum.Parse(typeof(Direction), Console.ReadLine());
tree = mananger.BinTreeThreadAddNode(tree, node, parentData, direction);
Console.WriteLine("插入成功,是否繼續? 1 繼續, 2 退出");
if (int.Parse(Console.ReadLine()) == 1)
continue;
else
break;
}
return tree;
}
#endregion
}
#region 節點標識(用于判斷孩子是節點還是線索)
/// <summary>
/// 節點標識(用于判斷孩子是節點還是線索)
/// </summary>
public enum NodeFlag
{
SubTree = 1,
Thread = 2
}
#endregion
#region 線索二叉樹的結構
/// <summary>
/// 線索二叉樹的結構
/// </summary>
/// <typeparam name="T"></typeparam>
public class ThreadTree<T>
{
public T data;
public ThreadTree<T> left;
public ThreadTree<T> right;
public NodeFlag leftFlag;
public NodeFlag rightFlag;
}
#endregion
#region 插入左節點或者右節點
/// <summary>
/// 插入左節點或者右節點
/// </summary>
public enum Direction { Left = 1, Right = 2 }
#endregion
#region 線索二叉樹的基本操作
/// <summary>
/// 線索二叉樹的基本操作
/// </summary>
public class ThreadTreeManager
{
#region 將指定節點插入到二叉樹中
/// <summary>
/// 將指定節點插入到二叉樹中
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="tree"></param>
/// <param name="node"></param>
/// <param name="direction">插入做左是右</param>
/// <returns></returns>
public ThreadTree<T> BinTreeThreadAddNode<T>(ThreadTree<T> tree, ThreadTree<T> node, T data, Direction direction)
{
if (tree == null)
return null;
if (tree.data.Equals(data))
{
switch (direction)
{
case Direction.Left:
if (tree.left != null)
throw new Exception("樹的左節點不為空,不能插入");
else
tree.left = node;
break;
case Direction.Right:
if (tree.right != null)
throw new Exception("樹的右節點不為空,不能插入");
else
tree.right = node;
break;
}
}
BinTreeThreadAddNode(tree.left, node, data, direction);
BinTreeThreadAddNode(tree.right, node, data, direction);
return tree;
}
#endregion
#region 中序遍歷構建線索二叉樹
/// <summary>
/// 中序遍歷構建線索二叉樹
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="tree"></param>
public void BinTreeThreadingCreate_LDR<T>(ref ThreadTree<T> tree, ref ThreadTree<T> prevNode)
{
if (tree == null)
return;
//先左子樹遍歷,尋找起始點
BinTreeThreadingCreate_LDR(ref tree.left, ref prevNode);
//如果left為空,則說明該節點可以放“線索”
tree.leftFlag = (tree.left == null) ? NodeFlag.Thread : NodeFlag.SubTree;
//如果right為空,則說明該節點可以放“線索”
tree.rightFlag = (tree.right == null) ? NodeFlag.Thread : NodeFlag.SubTree;
if (prevNode != null)
{
if (tree.leftFlag == NodeFlag.Thread)
tree.left = prevNode;
if (prevNode.rightFlag == NodeFlag.Thread)
prevNode.right = tree;
}
//保存前驅節點
prevNode = tree;
BinTreeThreadingCreate_LDR(ref tree.right, ref prevNode);
}
#endregion
#region 查找指定節點的后繼
/// <summary>
/// 查找指定節點的后繼
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="tree"></param>
public ThreadTree<T> BinTreeThreadNext_LDR<T>(ThreadTree<T> tree)
{
if (tree == null)
return null;
//如果查找節點的標志域中是Thread,則直接獲取
if (tree.rightFlag == NodeFlag.Thread)
return tree.right;
else
{
//根據中序遍歷的規則是尋找右子樹中中序遍歷的第一個節點
var rightNode = tree.right;
//如果該節點是subTree就需要循環遍歷
while (rightNode.leftFlag == NodeFlag.SubTree)
{
rightNode = rightNode.left;
}
return rightNode;
}
}
#endregion
#region 查找指定節點的前驅
/// <summary>
/// 查找指定節點的前驅
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="tree"></param>
/// <returns></returns>
public ThreadTree<T> BinTreeThreadPrev_LDR<T>(ThreadTree<T> tree)
{
if (tree == null)
return null;
//如果標志域中存放的是線索,那么可以直接找出來
if (tree.leftFlag == NodeFlag.Thread)
return tree.left;
else
{
//根據”中序“的規則可知,如果不為Thread,則要找出左子樹的最后節點
//也就是左子樹中最后輸出的元素
var leftNode = tree.left;
while (leftNode.rightFlag == NodeFlag.SubTree)
leftNode = leftNode.right;
return leftNode;
}
}
#endregion
#region 遍歷線索二叉樹
/// <summary>
/// 遍歷線索二叉樹
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="tree"></param>
public void BinTreeThread_LDR<T>(ThreadTree<T> tree)
{
if (tree == null)
return;
while (tree.leftFlag == NodeFlag.SubTree)
tree = tree.left;
do
{
Console.Write(tree.data + "/t");
tree = BinTreeThreadNext_LDR(tree);
} while (tree != null);
}
#endregion
}
#endregion
}
將文章開頭處的數據輸入到存儲結構中

新聞熱點
疑難解答