一: 最小生成樹
1. 概念
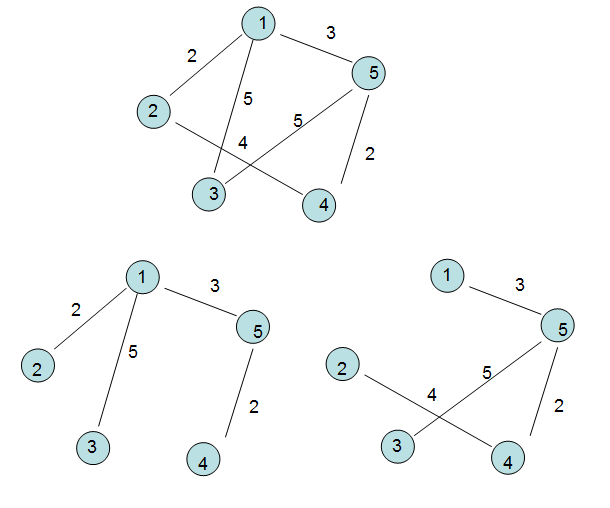
首先看如下圖,不知道大家能總結點什么。
對于一個連通圖G,如果其全部頂點和一部分邊構成一個子圖G1,當G1滿足:
① 剛好將圖中所有頂點連通。②頂點不存在回路。則稱G1就是G的“生成樹”。
其實一句話總結就是:生成樹是將原圖的全部頂點以最小的邊連通的子圖,這不,如下的連通圖可以得到下面的兩個生成樹。
② 對于一個帶權的連通圖,當生成的樹不同,各邊上的權值總和也不同,如果某個生成樹的權值最小,則它就是“最小生成樹”。
2. 場景
實際應用中“最小生成樹”還是蠻有實際價值的,教科書上都有這么一句話,若用圖來表示一個交通系統,每一個頂點代表一個城市,
邊代表兩個城市之間的距離,當有n個城市時,可能會有n(n-1)/2條邊,那么怎么選擇(n-1)條邊來使城市之間的總距離最小,其實它
的抽象模型就是求“最小生成樹”的問題。
3. prim算法
當然如何求“最小生成樹”問題,前人都已經給我們總結好了,我們只要照葫蘆畫瓢就是了,
第一步:我們建立集合“V,U",將圖中的所有頂點全部灌到V集合中,U集合初始為空。
第二步: 我們將V1放入U集合中并將V1頂點標記為已訪問。此時:U(V1)。
第三步: 我們尋找V1的鄰接點(V2,V3,V5),權值中發現(V1,V2)之間的權值最小,此時我們將V2放入U集合中并標記V2為已訪問,
此時為U(V1,V2)。
第四步: 我們找U集合中的V1和V2的鄰接邊,一陣痙攣后,發現(V1,V5)的權值最小,此時將V5加入到U集合并標記為已訪問,此時
U的集合元素為(V1,V2,V5)。
第五步:此時我們以(V1,V2,V5)為基準向四周尋找最小權值的鄰接邊,發現(V5,V4)的權值最小,此時將V4加入到U集合并標記
為已訪問,此時U的集合元素為(V1,V2,V5,V4)。
第六步: 跟第五步形式一樣,找到了(V1,V3)的權值最小,將V3加入到U集合中并標記為已訪問,最終U的元素為(V1,V2,V5,V4,V3),
最終發現頂點全部被訪問,最小生成樹就此誕生。
//非鄰接頂點標志
int noadj = -1;
//定義一個輸出總權值的變量
sum = 0;
//臨時數組,用于保存鄰接點的權值
int[] weight = new int[graph.vertexNum];
//臨時數組,用于保存頂點信息
int[] tempvertex = new int[graph.vertexNum];
//取出鄰接矩陣的第一行數據,也就是取出第一個頂點并將權和邊信息保存于臨時數據中
for (int i = 1; i < graph.vertexNum; i++)
{
//保存于鄰接點之間的權值
weight[i] = graph.edges[0, i];
//等于0則說明V1與該鄰接點沒有邊
if (weight[i] == short.MaxValue)
tempvertex[i] = noadj;
else
tempvertex[i] = int.Parse(graph.vertex[0]);
}
//從集合V中取出V1節點,只需要將此節點設置為已訪問過,weight為0集合
var index = tempvertex[0] = used;
var min = weight[0] = short.MaxValue;
//在V的鄰接點中找權值最小的節點
for (int i = 1; i < graph.vertexNum; i++)
{
index = i;
min = short.MaxValue;
for (int j = 1; j < graph.vertexNum; j++)
{
//用于找出當前節點的鄰接點中權值最小的未訪問點
if (weight[j] < min && tempvertex[j] != 0)
{
min = weight[j];
index = j;
}
}
//累加權值
sum += min;
Console.Write("({0},{1}) ", tempvertex[index], graph.vertex[index]);
//將取得的最小節點標識為已訪問
weight[index] = short.MaxValue;
tempvertex[index] = 0;
//從最新的節點出發,將此節點的weight比較賦值
for (int j = 0; j < graph.vertexNum; j++)
{
//已當前節點為出發點,重新選擇最小邊
if (graph.edges[index, j] < weight[j] && tempvertex[j] != used)
{
weight[j] = graph.edges[index, j];
//這里做的目的將較短的邊覆蓋點上一個節點的鄰接點中的較長的邊
tempvertex[j] = int.Parse(graph.vertex[index]);
}
}
}
}
#endregion
二: 最短路徑
1. 概念
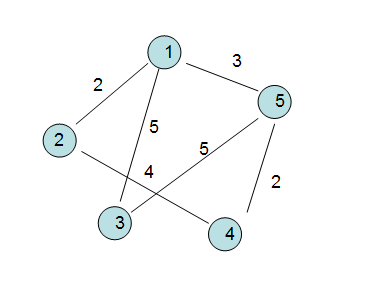
求最短路徑問題其實也是非常有實用價值的,映射到交通系統圖中,就是求兩個城市間的最短路徑問題,還是看這張圖,我們可以很容易的看出比如
V1到圖中各頂點的最短路徑。
① V1 -> V2 直達, 權為2。
② V1 -> V3 直達 權為3。
③ V1->V5->V4 中轉 權為3+2=5。
④ V1 -> V5 直達 權為3。
 、
、
2. Dijkstra算法
我們的學習需要站在巨人的肩膀上,那么對于現實中非常復雜的問題,我們肯定不能用肉眼看出來,而是根據一定的算法推導出來的。
Dijkstra思想遵循 “走一步,看一步”的原則。
第一步: 我們需要一個集合U,然后將V1放入U集合中,既然走了一步,我們就要看一步,就是比較一下V1的鄰接點(V2,V3,V5),
發現(V1,V2)的權值最小,此時我們將V2放入U集合中,表示我們已經找到了V1到V2的最短路徑。
第二步:然后將V2做中間點,繼續向前尋找權值最小的鄰接點,發現只有V4可以連通,此時修改V4的權值為(V1,V2)+(V2,V4)=6。
此時我們就要看一步,發現V1到(V3,V4,V5)中權值最小的是(V1,V5),此時將V5放入U集合中,表示我們已經找到了
V1到V5的最短路徑。
第三步:然后將V5做中間點,繼續向前尋找權值最小的鄰接點,發現能連通的有V3,V4,當我們正想修該V3的權值時發現(V1,V3)的權值
小于(V1->V5->V3),此時我們就不修改,將V3放入U集合中,最后我們找到了V1到V3的最短路徑。
第四步:因為V5還沒有走完,所以繼續用V5做中間點,此時只能連通(V5,V4),當要修改權值的時候,發現原來的V4權值為(V1,V2)+(V2,V4),而
現在的權值為5,小于先前的6,此時更改原先的權值變為5,將V4放入集合中,最后我們找到了V1到V4的最短路徑。
int[] path = new int[g.vertexNum];
int[] tempvertex = new int[g.vertexNum];
Console.WriteLine("/n請輸入源點的編號:");
//讓用戶輸入要遍歷的起始點
int vertex = int.Parse(Console.ReadLine()) - 1;
for (int i = 0; i < g.vertexNum; i++)
{
//初始賦權值
weight[i] = g.edges[vertex, i];
if (weight[i] < short.MaxValue && weight[i] > 0)
path[i] = vertex;
tempvertex[i] = 0;
}
tempvertex[vertex] = 1;
weight[vertex] = 0;
for (int i = 0; i < g.vertexNum; i++)
{
int min = short.MaxValue;
int index = vertex;
for (int j = 0; j < g.vertexNum; j++)
{
//頂點的權值中找出最小的
if (tempvertex[j] == 0 && weight[j] < min)
{
min = weight[j];
index = j;
}
}
tempvertex[index] = 1;
//以當前的index作為中間點,找出最小的權值
for (int j = 0; j < g.vertexNum; j++)
{
if (tempvertex[j] == 0 && weight[index] + g.edges[index, j] < weight[j])
{
weight[j] = weight[index] + g.edges[index, j];
path[j] = index;
}
}
}
Console.WriteLine("/n頂點{0}到各頂點的最短路徑為:(終點 < 源點) " + g.vertex[vertex]);
//最后輸出
for (int i = 0; i < g.vertexNum; i++)
{
if (tempvertex[i] == 1)
{
var index = i;
while (index != vertex)
{
var j = index;
Console.Write("{0} < ", g.vertex[index]);
index = path[index];
}
Console.WriteLine("{0}/n", g.vertex[index]);
}
else
{
Console.WriteLine("{0} <- {1}: 無路徑/n", g.vertex[i], g.vertex[vertex]);
}
}
}
#endregion
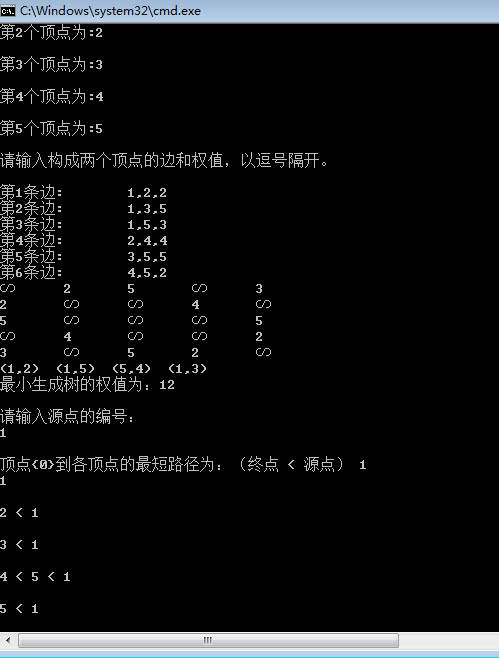
最后上一下總的運行代碼
namespace MatrixGraph
{
public class Program
{
static void Main(string[] args)
{
MatrixGraphManager manager = new MatrixGraphManager();
//創建圖
MatrixGraph graph = manager.CreateMatrixGraph();
manager.OutMatrix(graph);
int sum = 0;
manager.Prim(graph, out sum);
Console.WriteLine("/n最小生成樹的權值為:" + sum);
manager.Dijkstra(graph);
//Console.Write("廣度遞歸:/t");
//manager.BFSTraverse(graph);
//Console.Write("/n深度遞歸:/t");
//manager.DFSTraverse(graph);
Console.ReadLine();
}
}
#region 鄰接矩陣的結構圖
/// <summary>
/// 鄰接矩陣的結構圖
/// </summary>
public class MatrixGraph
{
//保存頂點信息
public string[] vertex;
//保存邊信息
public int[,] edges;
//深搜和廣搜的遍歷標志
public bool[] isTrav;
//頂點數量
public int vertexNum;
//邊數量
public int edgeNum;
//圖類型
public int graphType;
/// <summary>
/// 存儲容量的初始化
/// </summary>
/// <param name="vertexNum"></param>
/// <param name="edgeNum"></param>
/// <param name="graphType"></param>
public MatrixGraph(int vertexNum, int edgeNum, int graphType)
{
this.vertexNum = vertexNum;
this.edgeNum = edgeNum;
this.graphType = graphType;
vertex = new string[vertexNum];
edges = new int[vertexNum, vertexNum];
isTrav = new bool[vertexNum];
}
}
#endregion
/// <summary>
/// 圖的操作類
/// </summary>
public class MatrixGraphManager
{
#region 圖的創建
/// <summary>
/// 圖的創建
/// </summary>
/// <param name="g"></param>
public MatrixGraph CreateMatrixGraph()
{
Console.WriteLine("請輸入創建圖的頂點個數,邊個數,是否為無向圖(0,1來表示),已逗號隔開。");
var initData = Console.ReadLine().Split(',').Select(i => int.Parse(i)).ToList();
MatrixGraph graph = new MatrixGraph(initData[0], initData[1], initData[2]);
//我們默認“正無窮大為沒有邊”
for (int i = 0; i < graph.vertexNum; i++)
{
for (int j = 0; j < graph.vertexNum; j++)
{
graph.edges[i, j] = short.MaxValue;
}
}
Console.WriteLine("請輸入各頂點信息:");
for (int i = 0; i < graph.vertexNum; i++)
{
Console.Write("/n第" + (i + 1) + "個頂點為:");
var single = Console.ReadLine();
//頂點信息加入集合中
graph.vertex[i] = single;
}
Console.WriteLine("/n請輸入構成兩個頂點的邊和權值,以逗號隔開。/n");
for (int i = 0; i < graph.edgeNum; i++)
{
Console.Write("第" + (i + 1) + "條邊:/t");
initData = Console.ReadLine().Split(',').Select(j => int.Parse(j)).ToList();
int start = initData[0];
int end = initData[1];
int weight = initData[2];
//給矩陣指定坐標位置賦值
graph.edges[start - 1, end - 1] = weight;
//如果是無向圖,則數據呈“二,四”象限對稱
if (graph.graphType == 1)
{
graph.edges[end - 1, start - 1] = weight;
}
}
return graph;
}
#endregion
#region 輸出矩陣數據
/// <summary>
/// 輸出矩陣數據
/// </summary>
/// <param name="graph"></param>
public void OutMatrix(MatrixGraph graph)
{
for (int i = 0; i < graph.vertexNum; i++)
{
for (int j = 0; j < graph.vertexNum; j++)
{
if (graph.edges[i, j] == short.MaxValue)
Console.Write("∽/t");
else
Console.Write(graph.edges[i, j] + "/t");
}
//換行
Console.WriteLine();
}
}
#endregion
#region 廣度優先
/// <summary>
/// 廣度優先
/// </summary>
/// <param name="graph"></param>
public void BFSTraverse(MatrixGraph graph)
{
//訪問標記默認初始化
for (int i = 0; i < graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍歷每個頂點
for (int i = 0; i < graph.vertexNum; i++)
{
//廣度遍歷未訪問過的頂點
if (!graph.isTrav[i])
{
BFSM(ref graph, i);
}
}
}
/// <summary>
/// 廣度遍歷具體算法
/// </summary>
/// <param name="graph"></param>
public void BFSM(ref MatrixGraph graph, int vertex)
{
//這里就用系統的隊列
Queue<int> queue = new Queue<int>();
//先把頂點入隊
queue.Enqueue(vertex);
//標記此頂點已經被訪問
graph.isTrav[vertex] = true;
//輸出頂點
Console.Write(" ->" + graph.vertex[vertex]);
//廣度遍歷頂點的鄰接點
while (queue.Count != 0)
{
var temp = queue.Dequeue();
//遍歷矩陣的橫坐標
for (int i = 0; i < graph.vertexNum; i++)
{
if (!graph.isTrav[i] && graph.edges[temp, i] != 0)
{
graph.isTrav[i] = true;
queue.Enqueue(i);
//輸出未被訪問的頂點
Console.Write(" ->" + graph.vertex[i]);
}
}
}
}
#endregion
#region 深度優先
/// <summary>
/// 深度優先
/// </summary>
/// <param name="graph"></param>
public void DFSTraverse(MatrixGraph graph)
{
//訪問標記默認初始化
for (int i = 0; i < graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍歷每個頂點
for (int i = 0; i < graph.vertexNum; i++)
{
//廣度遍歷未訪問過的頂點
if (!graph.isTrav[i])
{
DFSM(ref graph, i);
}
}
}
#region 深度遞歸的具體算法
/// <summary>
/// 深度遞歸的具體算法
/// </summary>
/// <param name="graph"></param>
/// <param name="vertex"></param>
public void DFSM(ref MatrixGraph graph, int vertex)
{
Console.Write("->" + graph.vertex[vertex]);
//標記為已訪問
graph.isTrav[vertex] = true;
//要遍歷的六個點
for (int i = 0; i < graph.vertexNum; i++)
{
if (graph.isTrav[i] == false && graph.edges[vertex, i] != 0)
{
//深度遞歸
DFSM(ref graph, i);
}
}
}
#endregion
#endregion
#region prim算法獲取最小生成樹
/// <summary>
/// prim算法獲取最小生成樹
/// </summary>
/// <param name="graph"></param>
public void Prim(MatrixGraph graph, out int sum)
{
//已訪問過的標志
int used = 0;
//非鄰接頂點標志
int noadj = -1;
//定義一個輸出總權值的變量
sum = 0;
//臨時數組,用于保存鄰接點的權值
int[] weight = new int[graph.vertexNum];
//臨時數組,用于保存頂點信息
int[] tempvertex = new int[graph.vertexNum];
//取出鄰接矩陣的第一行數據,也就是取出第一個頂點并將權和邊信息保存于臨時數據中
for (int i = 1; i < graph.vertexNum; i++)
{
//保存于鄰接點之間的權值
weight[i] = graph.edges[0, i];
//等于0則說明V1與該鄰接點沒有邊
if (weight[i] == short.MaxValue)
tempvertex[i] = noadj;
else
tempvertex[i] = int.Parse(graph.vertex[0]);
}
//從集合V中取出V1節點,只需要將此節點設置為已訪問過,weight為0集合
var index = tempvertex[0] = used;
var min = weight[0] = short.MaxValue;
//在V的鄰接點中找權值最小的節點
for (int i = 1; i < graph.vertexNum; i++)
{
index = i;
min = short.MaxValue;
for (int j = 1; j < graph.vertexNum; j++)
{
//用于找出當前節點的鄰接點中權值最小的未訪問點
if (weight[j] < min && tempvertex[j] != 0)
{
min = weight[j];
index = j;
}
}
//累加權值
sum += min;
Console.Write("({0},{1}) ", tempvertex[index], graph.vertex[index]);
//將取得的最小節點標識為已訪問
weight[index] = short.MaxValue;
tempvertex[index] = 0;
//從最新的節點出發,將此節點的weight比較賦值
for (int j = 0; j < graph.vertexNum; j++)
{
//已當前節點為出發點,重新選擇最小邊
if (graph.edges[index, j] < weight[j] && tempvertex[j] != used)
{
weight[j] = graph.edges[index, j];
//這里做的目的將較短的邊覆蓋點上一個節點的鄰接點中的較長的邊
tempvertex[j] = int.Parse(graph.vertex[index]);
}
}
}
}
#endregion
#region dijkstra求出最短路徑
/// <summary>
/// dijkstra求出最短路徑
/// </summary>
/// <param name="g"></param>
public void Dijkstra(MatrixGraph g)
{
int[] weight = new int[g.vertexNum];
int[] path = new int[g.vertexNum];
int[] tempvertex = new int[g.vertexNum];
Console.WriteLine("/n請輸入源點的編號:");
//讓用戶輸入要遍歷的起始點
int vertex = int.Parse(Console.ReadLine()) - 1;
for (int i = 0; i < g.vertexNum; i++)
{
//初始賦權值
weight[i] = g.edges[vertex, i];
if (weight[i] < short.MaxValue && weight[i] > 0)
path[i] = vertex;
tempvertex[i] = 0;
}
tempvertex[vertex] = 1;
weight[vertex] = 0;
for (int i = 0; i < g.vertexNum; i++)
{
int min = short.MaxValue;
int index = vertex;
for (int j = 0; j < g.vertexNum; j++)
{
//頂點的權值中找出最小的
if (tempvertex[j] == 0 && weight[j] < min)
{
min = weight[j];
index = j;
}
}
tempvertex[index] = 1;
//以當前的index作為中間點,找出最小的權值
for (int j = 0; j < g.vertexNum; j++)
{
if (tempvertex[j] == 0 && weight[index] + g.edges[index, j] < weight[j])
{
weight[j] = weight[index] + g.edges[index, j];
path[j] = index;
}
}
}
Console.WriteLine("/n頂點{0}到各頂點的最短路徑為:(終點 < 源點) " + g.vertex[vertex]);
//最后輸出
for (int i = 0; i < g.vertexNum; i++)
{
if (tempvertex[i] == 1)
{
var index = i;
while (index != vertex)
{
var j = index;
Console.Write("{0} < ", g.vertex[index]);
index = path[index];
}
Console.WriteLine("{0}/n", g.vertex[index]);
}
else
{
Console.WriteLine("{0} <- {1}: 無路徑/n", g.vertex[i], g.vertex[vertex]);
}
}
}
#endregion
}
}
算法速成系列至此就全部結束了,公司給我們的算法培訓也于上周五結束,呵呵,趕一下同步。最后希望大家能對算法重視起來,
學好算法,終身收益。
新聞熱點
疑難解答