在本站上一篇文章中探討了在R中求解一元方程的方法，本文將進一步探討R中求解線性方程組的方法。

設有n個未知數的m個方程的線性方程組：

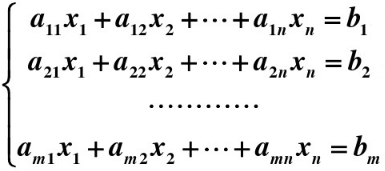
可以抽象成下列的形式：

A_m×n X_n×1 = b_m×1

對于該方程組

有唯一解的充分必要條件是R(A) = R(A, b) = n；

有無限多解的充分必要條件是 R(A) = R(A, b) < n；

無解的充分必要條件是 R(A) < R(A, b)

即：其有解的充分必要條件是R(A) = R(A, b)

當n=m時，方程為恰定方程組，則X = A^-1b；

當n<m時，方程組為超定方程組，則X = (A^TA)^-1A^Tb

當n>m時，方程數少于未知量個數，為欠定方程組，有無窮多個解。

1、直接使用矩陣相關知識來求解

（1）恰定方程組

如求下面的方程組：

在R中的求解過程如下：

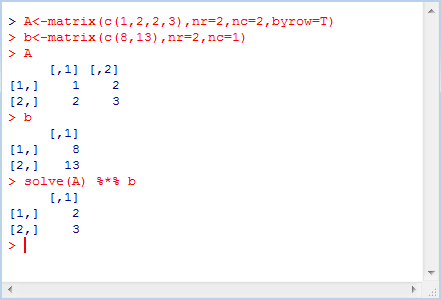
從圖中可以看出該方程組的解為：x1=2，x2=3。

（2）超定方程組

如求下面方程組的解：

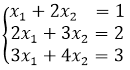
編寫R程序如下：

A<-matrix(c(1,2,2,3,3,4),nr=3,nc=2,byrow=T)
b<-matrix(c(1,2,3),nr=3,nc=1)
x<-solve(t(A)%*%A)%*%(t(A)%*%b)
x

運行結果如下圖所示：

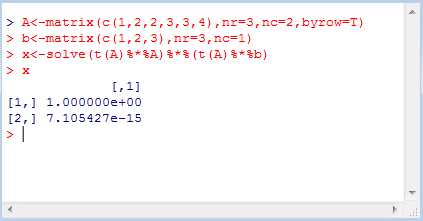
如上圖所示可知：該方程的解是x1=1，x2=0

 （3）欠定方程組求解

對于欠定方程組，即方程個數少于變量個數的方程組，可以使用SVD法求解。關于SVD的介紹，大家可以參照這個網址中的介紹：

https://blog.csdn.net/youngpan1101/article/details/54574130

如求解

可以編寫代碼如下：

A<-matrix(c(1,2,3,2,3,4),nr=2,nc=3,byrow=T)
b<-matrix(c(1,2),nr=2,nc=1)

#對A進行SVD分解
sol.svd <- svd(A)
#獲取U D V各個值
U<-sol.svd$u
D<-sol.svd$d
V<-sol.svd$v
C<-t(U)%*%b
Y<-C/D
X<-V%*%Y
X

求得的結果如下圖所示：

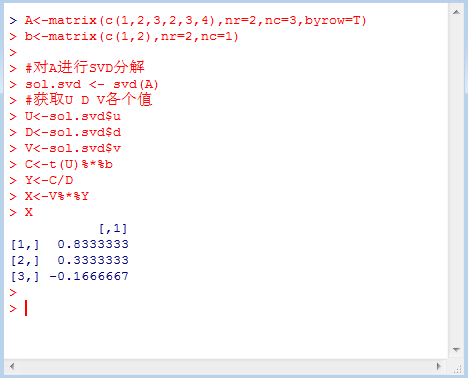
上圖求得的一個解是：x1=0.83,x2=0.33,x3=-0.17

對于R(A) = R(A, b) < n的方程組都可以使用這個方法進行求解。

再如下面的例子：

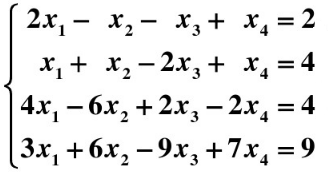
求解過程如下圖所示：

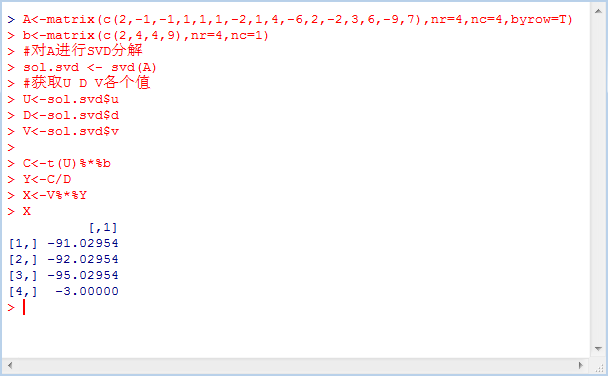
2、使用solve函數來求解

對于R(A) = R(A,b) = n的方程組，可以使用R中提供的solve函數直接求解。

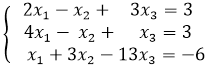
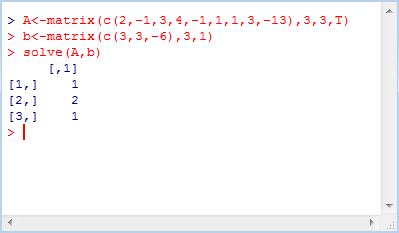
求解代碼如下：

A<-matrix(c(2,-1,3,4,-1,1,1,3,-13),3,3,T)
b<-matrix(c(3,3,-6),3,1)
solve(A,b)

運行結果如下：