所謂排列,就是指從給定個(gè)數(shù)的元素中取出指定個(gè)數(shù)的元素進(jìn)行排序。組合則是指從給定個(gè)數(shù)的元素中僅僅取出指定個(gè)數(shù)的元素,不考慮排序。(摘自百度百科)
1、排列的定義及公式
從n個(gè)不同元素中,任取r(m≤r,r與n均為自然數(shù),下同)個(gè)元素按照一定的順序排成一列,叫做從n個(gè)不同元素中取出r個(gè)元素的一個(gè)排列;從n個(gè)不同元素中取出r(r≤n)個(gè)元素的所有排列的個(gè)數(shù),叫做從n個(gè)不同元素中取出r個(gè)元素的排列數(shù),用符號(hào) p(n,r)表示。
其公式為:
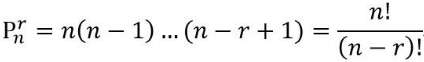
2、組合的定義及公式
從n個(gè)不同元素中,任取r(r≤n)個(gè)元素并成一組,叫做從n個(gè)不同元素中取出r個(gè)元素的一個(gè)組合;從n個(gè)不同元素中取出r(r≤n)個(gè)元素的所有組合的個(gè)數(shù),叫做從n個(gè)不同元素中取出r個(gè)元素的組合數(shù)。用符號(hào) C(n,r) 表示。
計(jì)算公式為:
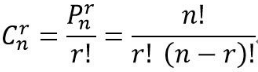
同時(shí),Crn = Cn-rn
在R中可以使用prod函數(shù)計(jì)算排列問題,使用choose函數(shù)計(jì)算組合問題。
1、prod函數(shù)
prod函數(shù)計(jì)算數(shù)字的連乘積。其格式如下:
prod(..., na.rm = FALSE)
其中,...是參與計(jì)算的數(shù)字(復(fù)數(shù)、邏輯)向量;na.rm表示是否忽略缺失值(NA),默認(rèn)為FALSE。
注意:當(dāng)na.rm為FALSE時(shí),參與計(jì)算的向量中若有NA值,則返回NA,否則會(huì)忽略向量中的NA值。
下面舉個(gè)例子說明該函數(shù)的使用:
> prod(1:8)
[1] 40320
上面這個(gè)例子相當(dāng)于計(jì)算8的階乘:8! = 40320
> prod(3:5)
[1] 60
上面這個(gè)例子相當(dāng)于計(jì)算:3 × 4 × 5 = 60
2、choose函數(shù)
choose函數(shù)的形式如下:
choose(n, k)
用于計(jì)算下列情形的問題:
n(n-1)…(n-k+1) / k! = n! / [(n-k)! k!] = C(n,k)
1、從1~5五個(gè)數(shù)字中,任意抽取2個(gè)不同的數(shù)字,一共有多少種數(shù)字組合方法。
這是組合問題,沒有順序問題,則C(5, 2) = 5!/(3!×2!) = 10,即有10中組合情況。
在R中計(jì)算如下:
> choose(5, 2)
[1] 10
在R中可以使用combn函數(shù)列出所有的組合情況,如本例中,可以使用下面的代碼,查看組合情況:
> combn(5, 2)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1 1 1 2 2 2 3 3 4
[2,] 2 3 4 5 3 4 5 4 5 5
2、從1~5五個(gè)數(shù)字中,任意抽取2個(gè)不同的數(shù)字,如果考慮兩個(gè)數(shù)字抽取的先后順序,則有多少種情況。
因?yàn)檫@里考慮了抽取數(shù)字的先后順序,是排列問題,則A(5,2) = 5! / (5-2)! = 20,即有20種組合順序。
可能的組合為:
(1,2),(1,3),(1,4),(1,5),
(2,1),(2,3),(2,4),(2,5),
(3,1),(3,2),(3,4),(3,5),
(4,1),(4,2),(4,3),(4,5),
(5,1),(5,2),(5,3),(5,4)
在R中計(jì)算如下:
> prod(1:5) / prod(1:3)
[1] 20
或者使用下面的R語句:
> choose(5,2) * prod(1:2)
[1] 20
也可以使用下面的R語句:
> choose(5,2) * factorial(2)
[1] 20
后面兩種情況,利用了排列和組合公式之間的關(guān)系進(jìn)行推導(dǎo)而來的。
在第3個(gè)R代碼中使用了factorial()函數(shù),該函數(shù)的作用計(jì)算某個(gè)數(shù)值的階乘,其原型如下:
factorial(x),這里當(dāng)x的值為0時(shí),則返回1.其余返回x(x-1)....1的連乘積,相當(dāng)于prod(1:x)
新聞熱點(diǎn)
疑難解答
圖片精選