1、什么是相關(guān)關(guān)系
相關(guān)分析(correlation analysis),從數(shù)量上分析現(xiàn)象之間相關(guān)關(guān)系的理論和方法。
現(xiàn)象之間的關(guān)系可以分為確定關(guān)系和非確定性關(guān)系。
確定性關(guān)系,可以說是函數(shù)關(guān)系,也就是說對(duì)于某一變量的每個(gè)數(shù)值都有另一變量的完全確定的值與之對(duì)應(yīng)。
非確定性關(guān)系,即這里所說的相關(guān)關(guān)系,現(xiàn)象之間存在一定的依存關(guān)系,但不是一一對(duì)應(yīng)的關(guān)系,即相隨變動(dòng)關(guān)系。
我們這里探討的就是相關(guān)分析。
2、相關(guān)關(guān)系的分類
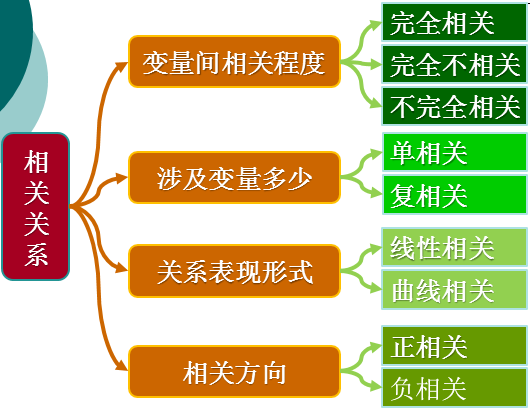
這篇文章主要研究線性相關(guān)關(guān)系
3、相關(guān)分析的基本步驟
(1)繪制散點(diǎn)圖,初步判斷兩個(gè)變量之間是否存在某種(線性)有規(guī)律的變化;
(2)正態(tài)性檢測(cè),如要選擇Pearson相關(guān)系數(shù),則要判斷兩個(gè)變量是否服從正態(tài)分布或近似正態(tài);
(3)計(jì)算相關(guān)系數(shù),選擇相關(guān)的方法公式來計(jì)算兩個(gè)變量的相關(guān)系數(shù)r;
(4)顯著性檢驗(yàn),判斷這種相關(guān)性是否顯著;
(5)給出結(jié)論。
4、散點(diǎn)圖
散點(diǎn)圖可以在坐標(biāo)系中表示因變量隨自變量而變化的大致趨勢(shì),據(jù)此可以選擇合適的函數(shù)對(duì)數(shù)據(jù)點(diǎn)進(jìn)行擬合。在R中繪制散點(diǎn)圖的方法可以參加本站中的另外一篇文章:《使用R語言繪制散點(diǎn)圖》
下圖的散點(diǎn)圖表示了兩個(gè)變量之間可能的情況:
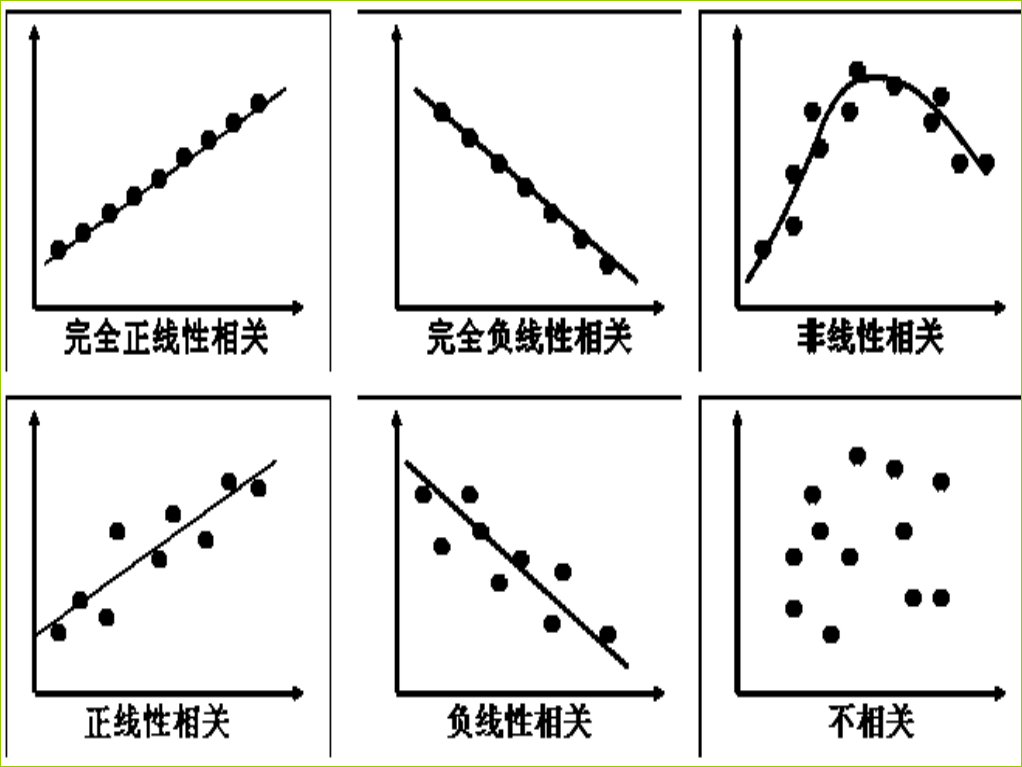
5、相關(guān)系數(shù)
相關(guān)系數(shù)(CorrelationCoefficient),是專門用來衡量?jī)蓚€(gè)變量之間的線性相關(guān)程度的指標(biāo),經(jīng)常用字母r來表示相關(guān)系數(shù)。
(1)Pearson相關(guān)系數(shù)
最常用的相關(guān)系數(shù),是皮爾遜(Pearson)相關(guān)系數(shù),又稱積差相關(guān)系數(shù),其公式如下:

(2)Spearman相關(guān)系數(shù)
用于兩個(gè)定序或定類變量的相關(guān)程序,對(duì)數(shù)據(jù)分布形態(tài)不作要求,也可以用于定序數(shù)據(jù),但不如Pearson精確。
秩相關(guān)系數(shù)的計(jì)算步驟如下:
1)把數(shù)量標(biāo)志和品質(zhì)標(biāo)志的具體表現(xiàn)按等級(jí)次序編號(hào);
2)按順序求出兩個(gè)標(biāo)志的每對(duì)等級(jí)編號(hào)的差;
3)按下式計(jì)算相關(guān)系數(shù):
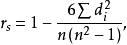
其中:秩相關(guān)系數(shù)記為rs,為兩變量每一對(duì)樣本的等級(jí)之差,即變量xi與yi的差值,n為樣本容量。
秩相關(guān)系數(shù)與相關(guān)系數(shù)一樣,取值-1到+1之間,rs為正時(shí)表示正相關(guān),rs為負(fù)時(shí)表示負(fù)相關(guān),rs等于零時(shí)表示相關(guān)為零。但與相關(guān)系數(shù)不同的是,它是建立在等級(jí)的基礎(chǔ)上計(jì)算的,較適用于反映序列變量的相關(guān)。
(3)Kendall相關(guān)系數(shù)
用于反映分類變量一致性的指標(biāo),兩個(gè)變量均屬于有序分類時(shí)使用,Kendall相關(guān)系數(shù)將在本站另行探討。
相關(guān)系數(shù)r主要特征有:
(1)取值范圍在[-1,1]之間。
(2)|r|越趨于1,表示線性相關(guān)越強(qiáng);|r|越趨于0,表示線性相關(guān)越弱。
(3)若|r|=1,為完全線性相關(guān)(相當(dāng)于兩變量是確定的函數(shù)關(guān)系)
(4)若r >0,表示兩個(gè)變量存在正相關(guān),若r<0,表示兩個(gè)變量存在負(fù)相關(guān),若r = 0,表示兩個(gè)變量不存在線性相關(guān)關(guān)系。
在實(shí)際中,將r分成幾個(gè)區(qū)間段來表示兩個(gè)變量之間的相關(guān)強(qiáng)度:
(1)|r|<0.3 相關(guān)極弱,為不存在線性相關(guān)關(guān)系;
(2)0.3 ≤ |r| < 0.5 為低度(弱)線性相關(guān);
(3)0.5 ≤ |r| <0.8為中度(顯著)線性相關(guān);
(4)|r| ≥0.8為高度線性相關(guān)。
相關(guān)分析與回歸分析在實(shí)際應(yīng)用中有密切關(guān)系。然而在回歸分析中,所關(guān)心的是一個(gè)隨機(jī)變量Y對(duì)還有一個(gè)(或一組)隨機(jī)變量X的依賴關(guān)系的函數(shù)形式。而在相關(guān)分析中 ,所討論的變量的地位一樣,分析側(cè)重于隨機(jī)變量之間的種種相關(guān)特征。比如,以X、Y分別記小學(xué)生的數(shù)學(xué)與語文成績(jī),感興趣的是二者的關(guān)系怎樣,而不在于由X去預(yù)測(cè)Y。
在R中可以使用cor函數(shù)計(jì)算兩組變量之間的相關(guān)系數(shù)。cor()函數(shù)的形式如下:
cor(x, y = NULL, use = "everything", method = c("pearson", "kendall", "spearman"))
其中,x為數(shù)值向量、矩陣或數(shù)據(jù)框;y默認(rèn)為NULL值,其為與x具有相同的維度;use是對(duì)缺失值的處理方式;method給出計(jì)算相關(guān)系數(shù)所使用的方法,即上面所探討的pearson相關(guān)系數(shù)、spearman相關(guān)系數(shù)和kendall相關(guān)系數(shù)。
下面舉例子來說明該函數(shù)的具體使用方法:
例1:假設(shè)對(duì)10戶居民家庭的月可支配收入和消費(fèi)支出進(jìn)行調(diào)查,得到的原始資料如下:
| 編號(hào) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 消費(fèi)支出 | 20 | 15 | 40 | 30 | 42 | 60 | 65 | 70 | 53 | 78 |
| 可支配收入 | 25 | 18 | 60 | 45 | 62 | 88 | 92 | 99 | 75 | 98 |
那么,居民的消費(fèi)支出與可支配收入之間是否存在線性相關(guān)關(guān)系,計(jì)算出相關(guān)系數(shù)并分析。
在R語言中編寫相關(guān)程序見下面:
x <- c(25,18,60,45,62,88,92,99,75,98) #定義向量x保存可支配收入
y <- c(20,15,40,30,42,60,65,70,53,78) #定義向量y保存消費(fèi)支出
#繪制散點(diǎn)圖,看看是否有線性關(guān)系
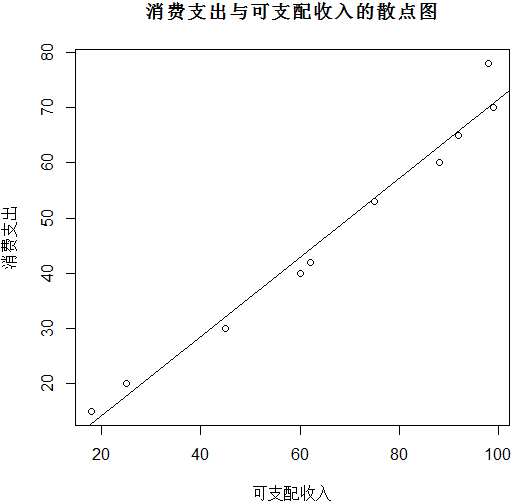
plot(x, y, xlab="可支配收入", ylab="消費(fèi)支出", main="消費(fèi)支出與可支配收入的散點(diǎn)圖")
#這樣從散點(diǎn)圖可以看出大致是否成線性關(guān)系,是正相關(guān)還是負(fù)相關(guān)
#還可以在散點(diǎn)圖中添加趨勢(shì)線,觀察大體趨勢(shì)
abline(lm(y~x)) #添加趨勢(shì)線,lm()是繪制y與x之間的線性方程
#正態(tài)性檢驗(yàn)
#計(jì)算的W值越接近1,表明越接近正態(tài)性
shapiro.test(x) #檢驗(yàn)x是否符合正態(tài)分布要求
shapiro.test(y) #檢驗(yàn)y是否符合正態(tài)分布要求
cor(x,y) #計(jì)算相關(guān)系數(shù),默認(rèn)采用pearson相關(guān)系數(shù)
#可以使用method參數(shù)指定計(jì)算的系數(shù)類型
cor(x,y,method='pearson') #pearson法計(jì)算的相關(guān)系數(shù)
#相關(guān)性的顯著性檢驗(yàn):原假設(shè)為變量間不相關(guān)
#使用cor.test()函數(shù)
cor.test(x,y) #默認(rèn)使用pearson方法進(jìn)行檢驗(yàn)
cor.test(x,y,method="pearson") #可以指定使用pearson方法進(jìn)行檢驗(yàn)
繪制的散點(diǎn)圖如下:
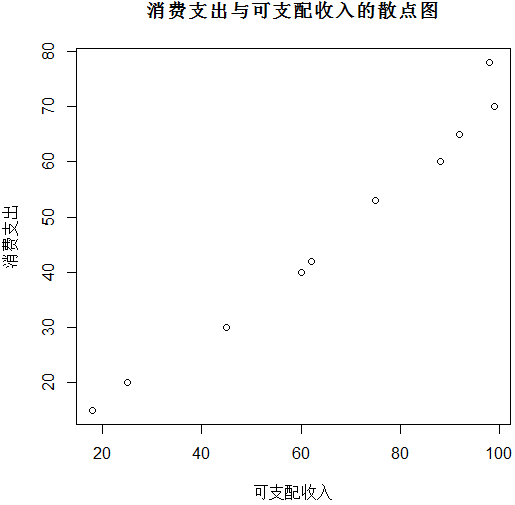
添加趨勢(shì)線后的散點(diǎn)圖:
正態(tài)性檢驗(yàn)的結(jié)果:

正態(tài)性原假設(shè)為總體服從正態(tài)分布,從檢驗(yàn)結(jié)果來看,兩變量的p-value均大于0.05,則在0.05的顯著性水平下,不能拒絕原假設(shè),即認(rèn)為兩個(gè)變量服從正態(tài)分布。
相關(guān)系數(shù)計(jì)算結(jié)果如下:
0.9877601
可以看出兩個(gè)變量具有高度相關(guān)性,且相關(guān)系數(shù)大于0,則居民支出與銷售收入具有高度的正相關(guān)性。
顯著性檢驗(yàn)結(jié)果:

從檢驗(yàn)結(jié)果來看,p值<0.05,則在0.05的顯著性水平下,相關(guān)系數(shù)較顯著。
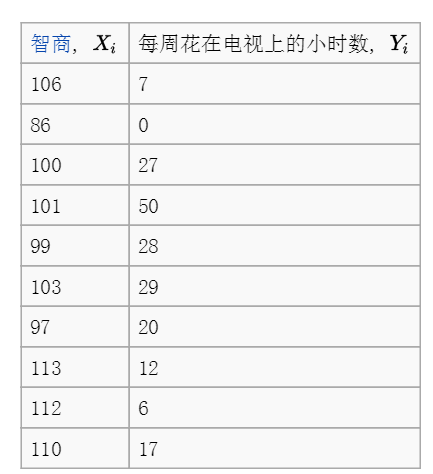
例2:檢驗(yàn)智商和其每周花在 電視上的小時(shí)數(shù)的相關(guān)性,其數(shù)據(jù)如下:
編寫r程序如下:
#定義數(shù)據(jù)
x <- c(106,86,100,101,99,103,97,113,112,110)
y <- c(7,0,27,50,28,29,20,12,6,17)
#計(jì)算相關(guān)系數(shù)
cor(x,y,method="spearman")
#顯著性檢驗(yàn)
cor.test(x,y,method="spearman")
相關(guān)系數(shù)計(jì)算結(jié)果如下:
-0.1757576
檢驗(yàn)結(jié)果如下圖:

從檢驗(yàn)結(jié)果來看,p值>0.05,則在0.05的顯著性水平下,不能拒絕原假設(shè),則相關(guān)系數(shù)不夠顯著。
上面的例子有些來源于網(wǎng)絡(luò)。
|
新聞熱點(diǎn)
疑難解答
圖片精選