1、方差分析的基本概念
方差分析(Analysis of Variance, ANOVA),由英國統(tǒng)計學家費雪(Ronald Aylmer Fisher)于1920年前后提出,最初主要應(yīng)用于生物和農(nóng)業(yè)田間試驗,后來推廣到各個領(lǐng)域。
它直接對多個總體的均值是否相等進行檢驗。
方差分析能夠解決多個均值是否相等的檢驗問題。
方差分析是要檢驗各個水平的均值是否相等,采用的方法是比較各水平的方差。
如研究不同的銷售點(假設(shè)為5個)對銷售量是否有有影響,可以收集不同銷售點若干天的銷售數(shù)據(jù)來進行研究,則實質(zhì)上是看這些銷售點在這些天中的平均銷售量 是否相同(或由顯著差異)。
所要檢驗的對象稱為因素或因子,也稱為自變量。如例子中的銷售點就是因素。
因素的不同表現(xiàn)稱為水平或處理 。如例子中研究的是5個銷售點,則共有5個水平。
每個因素水平下得到的樣本數(shù)值稱為觀測值 ,也稱為因變量或響應(yīng)變量。
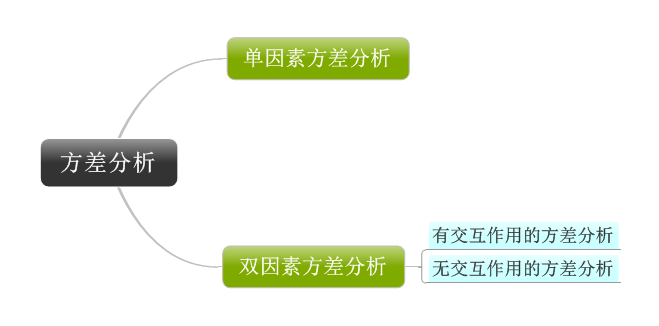
如果研究中只考慮一個因素的話,稱之為單因素方差分析;如果考慮兩個因素的話,稱為雙因素方差分析;雙因素方差分析中如果不考慮兩個因素的交互作用對因變量的影響的話,稱之為無交互作用的雙因素方差分析,否則稱之為有交互作用的雙因素方差分析。
2、方差分析的原假設(shè)與備擇假設(shè)
原假設(shè):
H0: μ1= μ2 = μ3 = μ4 = ...... = μn
備擇假設(shè):
H1:均值不全相等。
3、方差分析運用的前提條件
(1)各樣本是相互獨立的隨機樣本——獨立性;
(2)各組的方差相同——方差齊性;
(3)各樣本來自正態(tài)分布——正態(tài)性。
4、單因素方差分析問題原型
研究僅涉及到一個因素。如例子中的研究僅考慮銷售點一個因素。
(1)問題原型
設(shè)因素A有r個水平A1,A2,...,Ar,每個水平Ai進行ni次獨立觀測,將水平Ai下的試驗結(jié)果xi1,xi2,...,xini看成來自第i個正態(tài)總體Xi~N(μi,σ)的樣本觀測值,其中μi,σ均未知,并且每個總體Xi都相互獨立。考慮線性統(tǒng)計模型:
xij = u i + εij
εij~N(0,σ2) 且相互獨立
其中,μi為第i個總體的均值,ε為相應(yīng)的試驗誤差。
(2)單因素方差分析的數(shù)據(jù)結(jié)構(gòu)
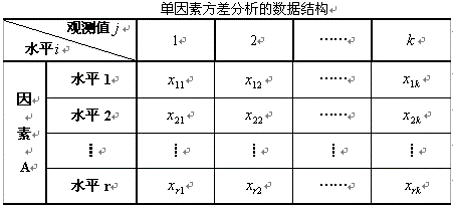
(3)單因素方差分析表
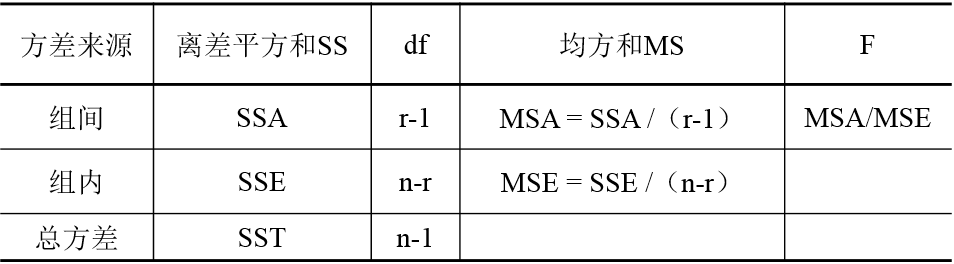
(4)判斷與結(jié)論
在假設(shè)條件成立時,F(xiàn)統(tǒng)計量服從第一自由度為r-1、第二自由度為n-r的 F分布。
若F ≥ Fα,則拒絕原假設(shè),表明均值之間的差異顯著,因素A對觀察值有顯著影響;
若F < Fα,則不能拒絕原假設(shè),表明均值之間的差異不顯著,因素A對觀察值沒有顯著影響。
5、R中進行方差分析的函數(shù)
在R中可以使用aov()函數(shù)和summary()函數(shù)共同完成方差分析的計算。aov()函數(shù)的格式如下:
aov(formula, data = NULL, projections = FALSE, qr = TRUE, contrasts = NULL, ...)
其中,formula是個字符串,表示方差分析的公式,如形如X~A或X~A+B或X~X+B+A:B;
data是數(shù)據(jù)框,描述數(shù)據(jù)的響應(yīng)變量、因素和相應(yīng)水平的對應(yīng)關(guān)系,默認值為NULL,當數(shù)據(jù)直接由X和A給出時,不需要此參數(shù)。
6、R語言進行單因素方差分析舉例說明
新實驗樓裝修,小明需要買一批燈泡。市場上的燈泡種類繁多,而且價格也相差較大。小明選擇了4種品牌的燈泡請人做了測試。測試結(jié)果如下表。你認為購買哪種品牌較好呢?
| 品牌 | 使用壽命 | |||||||
| A1 | 1600 | 1610 | 1650 | 1680 | 1700 | 1700 | 1780 | |
| A2 | 1500 | 1640 | 1400 | 1700 | 1750 | |||
| A3 | 1640 | 1550 | 1600 | 1620 | 1640 | 1600 | 1740 | 1800 |
| A4 | 1510 | 1520 | 1530 | 1570 | 1640 | 1600 | ||
當然選擇平均壽命要大一些的,那么這些水平均值有區(qū)別嗎?如何進行分析:方差分析。
在R中編寫程序如下:
#單因素方法分析
#定義數(shù)據(jù)燈泡壽命向量
X<-c(1600,1610,1650,1680,1700,1700,1780,
1500,1640,1400,1700,1750,
1640,1550,1600,1620,1640,1600,1740,1800,
1510,1520,1530,1570,1640,1600)
#定義一個因子用于指定每個數(shù)據(jù)所屬的組
A<-factor(rep(1:4,c(7,5,8,6))) #使用重復函數(shù)進行定義
#定義數(shù)據(jù)框
lamp<-data.frame(X,A)
#進行方差分析
lampAov<-aov(X~A,projections=F)
#提取方差分析表
sm<-summary(lampAov)
print(sm) #輸出方差分析信息
#數(shù)據(jù)滿足正態(tài)性要求嗎?
#對數(shù)據(jù)進行正態(tài)性符合性檢驗(Shapiro-Wilk)
#該檢驗中計算的W值越接近1,正態(tài)性越好
#對數(shù)據(jù)框中的X列值因素水平為1的進行正態(tài)性檢驗
shapiro.test(lamp$X[lamp$A==1])
#對數(shù)據(jù)框中的X列值因素水平為2的進行正態(tài)性檢驗
shapiro.test(lamp$X[lamp$A==2])
#對數(shù)據(jù)框中的X列值因素水平為3的進行正態(tài)性檢驗
shapiro.test(lamp$X[lamp$A==3])
#對數(shù)據(jù)框中的X列值因素水平為4的進行正態(tài)性檢驗
shapiro.test(lamp$X[lamp$A==4])
#當水平數(shù)較多時,運用上面的寫法比較麻煩,可以借助with()函數(shù)和tapply()函數(shù)
with(lamp,tapply(X,A,shapiro.test))
#方差齊性檢驗
bartlett.test(X~A,data=lamp)
在R中的運行結(jié)果如下:
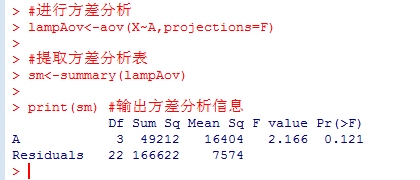
從結(jié)果中看,P值>0.05,則在0.05的顯著性水平下,沒有充分理由拒絕原假設(shè),也就是說4種品牌的壽命沒有顯著性區(qū)別,則在購買時,挑揀便宜的進行購買就行了。
正態(tài)性檢驗結(jié)果如下:

從檢驗結(jié)果來看,各組數(shù)據(jù)都符合正態(tài)性。
方差齊性檢驗結(jié)果:

由檢驗結(jié)果的p值=0.1215 > 0.05可知,在0.05的置信水平下,沒有充分理由拒絕原假設(shè)(每組的方差相等),則可以認為每組的方差相等,即滿足方差齊性。
新聞熱點
疑難解答