本站在《使用R語言進行單因素方差分析》一文中介紹了在R語言中使用aov函數進行方差分析的方法,并給出具體的例子講解了該函數的使用方法及其正態性檢驗和方差齊性檢驗的方法。在實際中,在進行單因素方差分析時,可能檢驗結果拒絕了零假設,即因素A的r個水平效應具有顯著的差異,也就是說r個均值之間有顯著區別。但這并不能說明r個均值之間都會存在這個顯著差異,只能說明至少2個總體的均值有顯著差異。那么,到底是哪些水平之間存在差異呢?我們需要對每兩個水平間的均值做一一比較,即多重比較。
同時比較任意兩個水平均值間有無明顯差異的問題稱為多重比較。通常采用多重T檢驗方法進行多重比較,這種方法本質上就是針對每組數據進行T檢驗,只不過估計方差時利用的是全體數據,因而自由度變大。具體地說,要比較第i個總體與第j個總體的均值是否相同,即檢驗:(薛毅,陳立萍.R語言在統計中的應用)
H0: μi = μj,H1:μi ≠ μj,i ≠ j,i,j=1,2,...,r
在R中,使用pairwise.t.test()函數可以幫助我們完成多重T檢驗,該函數的原型如下:
pairwise.t.test(x, g, p.adjust.method = p.adjust.methods, pool.sd = !paired,
paired = FALSE, alternative = c("two.sided", "less", "greater"), ...)
其中,主要參數的含義如下:
x 是一個向量,代表響應變量(因變量);
g 代表響應向量的因子或向量;
p.adjust.method 調整p值所使用的方法;
paired 邏輯變量,表示是否做成對的t檢驗,默認為FALSE,此變量和pool.sd不能同時為TRUE;
alternative 字符串,表示備擇假設。取值為two.sided(雙側檢驗),less(單側小于),greater(單側大于),默認為two.sided.
下面用一個例子來說明本函數的具體使用方法:
為了減小失業保險支出,促進就業,政府試圖為失業者提供再就業獎勵:如果失業者可以在限定的時間內重新就業,他將可以獲得一定數額的獎金,這個政策是否有效呢?下圖給出了不同獎勵下再就業的天數。
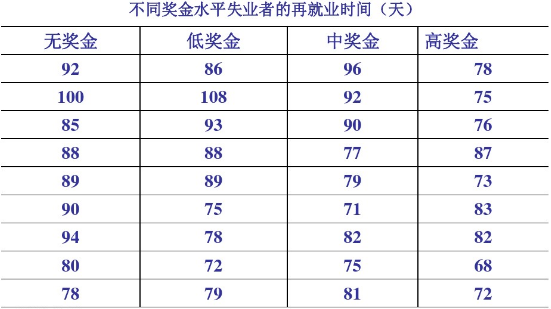
(本例子來源于網絡)
編寫程序如下:
#定義數據
x<-c(92,100,85,88,89,90,94,80,78,
86,108,93,88,89,75,78,72,79,
96,92,90,77,79,71,82,75,81,
78,75,76,87,73,83,82,68,72)
A<-factor(rep(1:4,c(9,9,9,9)))
#定義數據框
dat<-data.frame(x,A)
#方差分析
aovResult<-aov(x~A,data=dat)
#提取方差分析表
summary(aovResult)
#多重比較
pairwise.t.test(x,A)
方差分析結果如下圖所示:
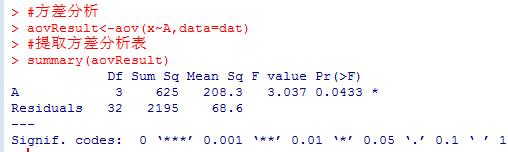
由上圖方差分析的結果來看,p值=0.0433<0.05,則可以認為有充分理由認為水平間的效用是不同的。
那么,不同產生在哪些水平間呢,下面是多重比較的結果:

從上圖可以看出1和4之間的p值為0.04,則可以認為有充足的理由認為水平1和水平4之間差異顯著,即無獎金組和高獎金組的再就業時間有顯著性差異。而其它組之間沒有差異。
上圖還給出了p值調整所用的方法:holm修正的方法。
因為在多重T檢驗時,當因素的水平較多,而檢驗又是同時進行的,則多次重復使用T檢驗會增大犯第一類錯誤的概率,得到的“有顯著差異”的結論不可靠。為了克服這一缺陷,統計學家提出了多種方法來調整P值,這里使用的是holm調整方法。
新聞熱點
疑難解答