雙因素方差分析就是考慮兩個因素的方差分析,兩個因素可以稱之為因素A和因素B,設因素A有r個水平A1,A2,...,Ar,因素B有s個水平B1,B2,...,Bs.
雙因素方差分析有兩種類型:
一種是無交互作用的雙因素方差分析,它假定因素A和因素B的效應之間是相互獨立的,不存在相互關系;
另一種是有交互作用的方差分析,它假定A、B兩個因素不是獨立的,而是相互起作用的,兩個因素同時起作用的結果不是兩個因素分別作用的簡單相加,兩者的結合會產(chǎn)生一個新的效應。
這種效應的最典型的例子是,耕地深度和施肥量都會影響產(chǎn)量,但同時深耕和適當?shù)氖┓士赡苁巩a(chǎn)量成倍增加,這時,耕地深度和施肥量就存在交互作用。兩個因素結合后就會產(chǎn)生出一個新的效應,屬于有交互作用的方差分析問題。
本文首先探討一下無交互作用的雙因素方差分析相關問題。
無交互作用的雙因素方差分析的數(shù)據(jù)結構表如下:
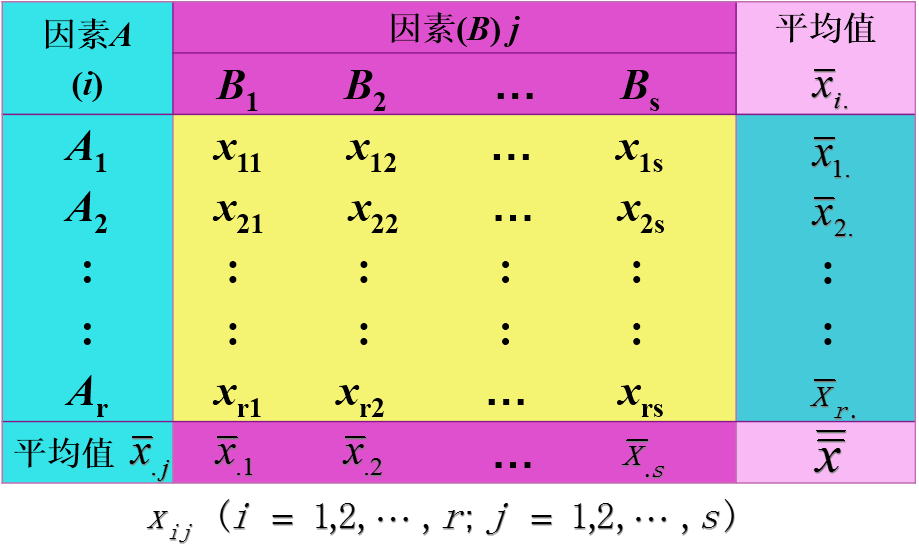
分析的步驟
(1)提出假設
對因素A提出的假設為:
H0: μ1 = μ2 = … = μi = …= μr (μi為第i個水平的均值)
H1: μi (i =1,2, … , r) 不全相等
對因素B提出的假設為:
H0: μ1 = μ2 = … = μj = …= μs (μj為第j個水平的均值)
H1: μj (j =1,2,…,s) 不全相等
(2)構造檢驗統(tǒng)計量
總離差平方和:
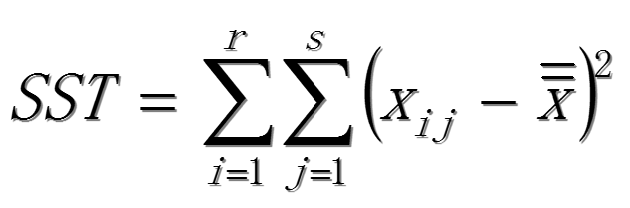
因素A的離差平方和SSA:
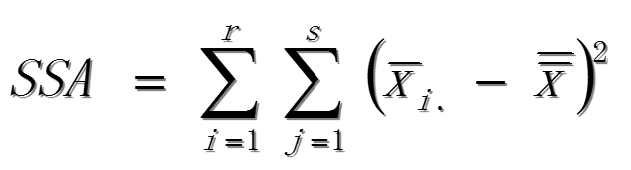
因素B的離差平方和SSB:
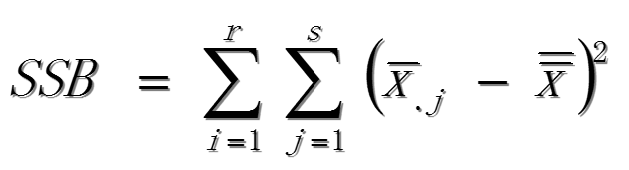
誤差項平方和SSE:
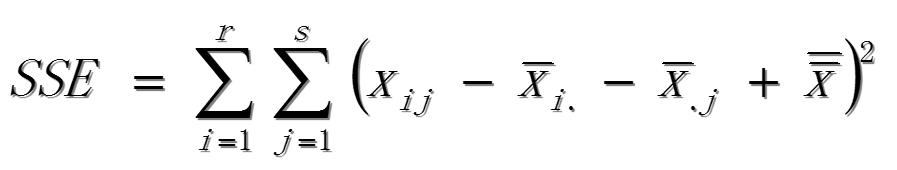
各平方和的關系:
SST = SSA + SSB + SSE
(3)計算均方MS
因素A的均方:
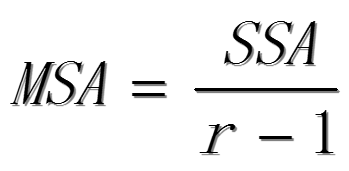
因素B的均方:
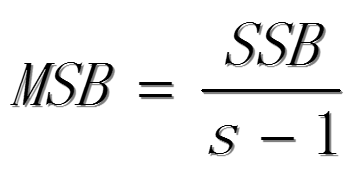
隨機誤差項的均方:
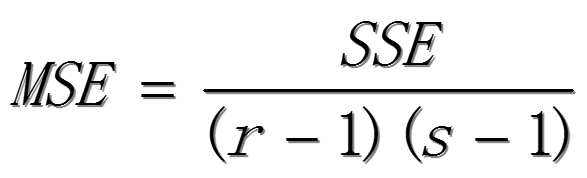
(4)計算檢驗統(tǒng)計量F

(5)統(tǒng)計決策
將統(tǒng)計量的值F與給定的顯著性水平α的臨界值Fα進行比較,作出接受或拒絕原假設H0的決策:
根據(jù)給定的顯著性水平α在F分布表中查找相應的臨界值 Fα
若FA≥ Fα,則拒絕原假設H0,表明均值之間的差異是顯著的,即所檢驗的因素(A)對觀察值有顯著影響
若FB≥Fα,則拒絕原假設H0,表明均值之間有顯著差異,即所檢驗的因素(B)對觀察值有顯著影響
無交互作用的方法分析表如下:
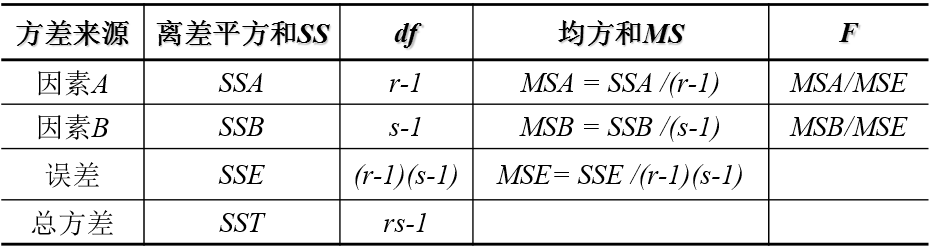
R語言中進行無交互作用的雙因素方差分析的方法
在R語言中,無交互作用的雙因素方差分析方法與單因素方差分析所使用的函數(shù)相同,即aov函數(shù)和summary函數(shù)。
下面舉例子來說明:
例1:某產(chǎn)品銷售量是否與銷售方式和銷售地點有關
某公司想知道產(chǎn)品銷售量與銷售方式及銷售地點是否有關,隨機抽樣得表中資料,以0.05的顯著性水平進行檢驗。
| 地點一 | 地點二 | 地點三 | 地點四 | 地點五 | |
| 方式一 | 77 | 86 | 81 | 88 | 83 |
| 方式二 | 95 | 92 | 78 | 96 | 89 |
| 方式三 | 71 | 76 | 68 | 81 | 74 |
| 方式四 | 80 | 84 | 79 | 70 | 82 |
在R中編寫程序如下所示:
#無重復作用的雙因素方差分析
#定義銷售量向量
X<-c(77,86,81,88,83,95,92,78,96,89,71,76,68,81,74,80,84,79,70,82)
A<-gl(4,5) #銷售方式四種
B<-gl(5,1,20) #銷售地點五個
sales<-data.frame(X,A,B) #創(chuàng)建數(shù)據(jù)框
sales.aov<-aov(X~A+B,data =sales)
summary(sales.aov)
運行結果如下圖所示:
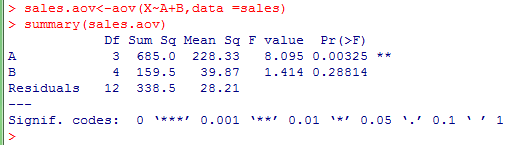
從分析結果來看,銷售方式的P值=0.00325<0.05,則認為因素A不同銷售方式對銷售量有顯著影響,而銷售地點的P值=0.28814>0.5,沒有充分理由說明銷售地點對銷售量有影響。
例2:食品包裝和銷售地區(qū)對某商品銷售量是否有影響
為研究食品的包裝和銷售地區(qū)對其銷售量是否有影響,在某周的三個不同地區(qū)中用三種不同包裝方法進行銷售,獲得的銷售量數(shù)據(jù)如下表。
| 銷售地區(qū)(A) | 包裝方法(B) | |||
| B1 | B2 | B3 | B4 | |
| A1 | 45 | 75 | 30 | 40 |
| A2 | 50 | 50 | 40 | 48 |
| A3 | 35 | 65 | 50 | 53 |
檢驗不同的地區(qū)和不同的包裝方法對該食品的銷售量是否有顯著影響? (α=0.05)
在R中編寫程序如下:
X<-c(45,75,30,40,50,50,40,48,35,65,50,53)
A<-c(1,1,1,1,2,2,2,2,3,3,3,3)
#或者A<-gl(4,4)
B<-rep(c(1:4),3)
#或者B<-gl(4,1,12)
dat<-data.frame(X,A,B)
re<-aov(X~A+B,data=dat)
summary(re)
分析結果如下:

從分析結果來看,因素A和因素B的P值均大于0.05,則可以認為因素A和因素B對食品銷售量沒有影響。
新聞熱點
疑難解答