在前面文章中介紹了雙因素方差分析的相關知識以及無交互作用的雙因素方差分析的相關理論,并給出了R語言的相關代碼。本文將進一步介紹一下有交互作用的雙因素方差分析方法,并在R中實現的基本方法。
關于無交互作用的方差分析方法,可參見本站的文章:使用R語言進行無交互作用的雙因素方差分析
在實際中,兩個因素往往對要研究的問題存在著交互影響,如適當的施肥量和降雨量對農作物的產量存在著交互影響。
有交互作用的方差分析表如下圖所示:
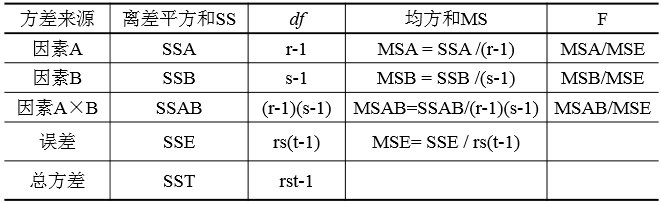
為檢驗因素A的影響是否顯著,采用統計量:
![]()
為檢驗因素B的影響是否顯著,采用統計量:
![]()
為檢驗因素A、B交互效應的影響是否顯著,采用統計量:
![]()
R語言中進行有交互作用的雙因素方差分析的方法
在R語言中,有交互作用的雙因素方差分析方法與無交互作用的雙因素方差分析所使用的函數相同,即aov函數和summary函數。
下面舉例子來說明:
例1:電池的板極材料與使用的環境溫度對電池的輸出電壓均有影響。
今材料類型與環境溫度都取了三個水平,測得輸出電壓數據如下表,問不同材料、不同溫度及它們的交互作用對輸出電壓有無顯著影響(α=0.05),數據如下圖所示:
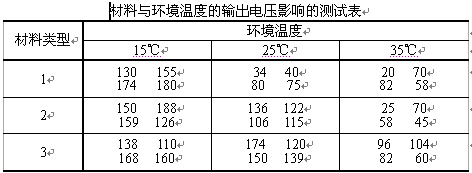
本例的數據保存在文本文件中,每個數據以空格隔開,有興趣的讀者可以點擊下面的鏈接進行下載實驗。
本例的數據文件下載(請右擊選擇連接另存為): 點擊下載此文件
點擊下載此文件
在R中編寫程序如下:
#####有交互作用的方差分析
#使用scan函數從文本文件中讀取數據
V<-scan("vmt.txt")
#定義材料因子
M<-gl(3,12,labels=c("M1","M2","M3"))
#定義溫度因子
T<-gl(3,4,labels=c("T1","T2","T3"))
#定義數據框
VMT<-data.frame(V, M, T)
#進行分析
fx<-aov(V~M+T+M:T, data=VMT)
summary(fx) #提取方差分析表
在上面的方差分析函數aov中,第一個參數使用了公式的形式:V~M+T+M:T,其中M:T表示兩個因素間的交互作用,如沒有這一項,則表示因素M和因素T的無交互作用的方差分析。
其運行結果如下:
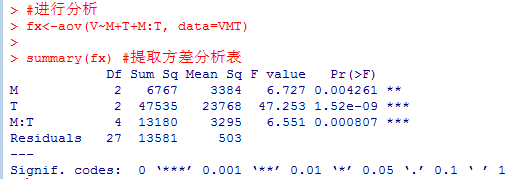
從上圖的結果來看,材料因素的Pr=0.004<0.05,則說明材料對輸出電壓的影響具有顯著性區別,溫度因素的pr=1.52e-09<0.05,則說明溫度對輸出電壓的影響非常顯著,M:T即材料和溫度的交互作用的pr=0.0008<0.05,說明兩者的交互作用對輸出電壓的影響也是顯著的。
例2:不同教學方法和教材對學習效果是否有影響。
用三種不同教材和兩種不同教學方法在6個小班重復實驗得到的數據如下:

問:教材,教法及兩者的交互作用是否對教學效果有影響。
教學效果的數據存儲在jxxg.txt文件中,以英文逗號(,)作為分隔符。可以點擊下面的鏈接進行下載:
教學效果數據文件下載(請右擊選擇連接另存為): 點擊下載此文件
點擊下載此文件
在R中編寫程序如下:
########有交互作用的方差分析
##教學方法和教材對教學效果的影響分析##
#從jxxg.txt文件中讀取數據
#每個數據以英文逗號(,)作為分隔
eff<-scan("jxxg.txt",sep=",")
#定義教材因子
jc<-gl(3,8,labels=c("B1","B2","B3"))
#定義教法因子
jf<-gl(2,4,length=24,labels=c("M1","M2"))
#定義數據框
JXXG<- data.frame(eff,jc,jf)
#進行方差分析
aova.double<-aov(eff~jc+jf+jc:jf,data=JXXG)
#提取方差分析表
summary(aova.double)
運行結果如下圖所示:
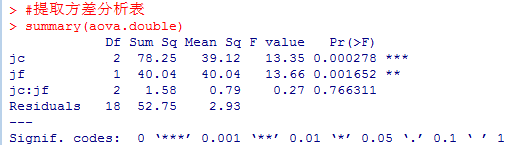
從上圖可以看出,jc(教材)因素和jf(教法)因素分別對教學效果有顯著影響,而兩者的交互作用對教學效果的影響不夠顯著。
新聞熱點
疑難解答